Uniform {stats} を利用して、連続一様分布の確率密度関数を確認します。
変数n,a,bを変更した場合のシミュレーションは https://www.webr.saecanet.com/webr-continuous-uniform-distribution で確認出来ます。
確率密度関数
$$\begin{equation}f(x)=\begin{cases}\dfrac{1}{b-a} & \textrm{for}\quad a \leq x \leq b\\0& \textrm{for}\quad x<a\; \textrm{or}\;x>b\end{cases}\end{equation}$$
累積分布関数
$$\begin{equation}F(x)=\begin{cases}0 & \textrm{for}\quad x<a\\ \dfrac{x-a}{b-a} & \textrm{for}\quad a \leq x < b\\1& \textrm{for}\quad x\geq b\end{cases}\end{equation}$$
期待値
$$E(x)=\dfrac{a+b}{2}$$
分散
$$V(x)=\dfrac{(b-a)^2}{12}$$
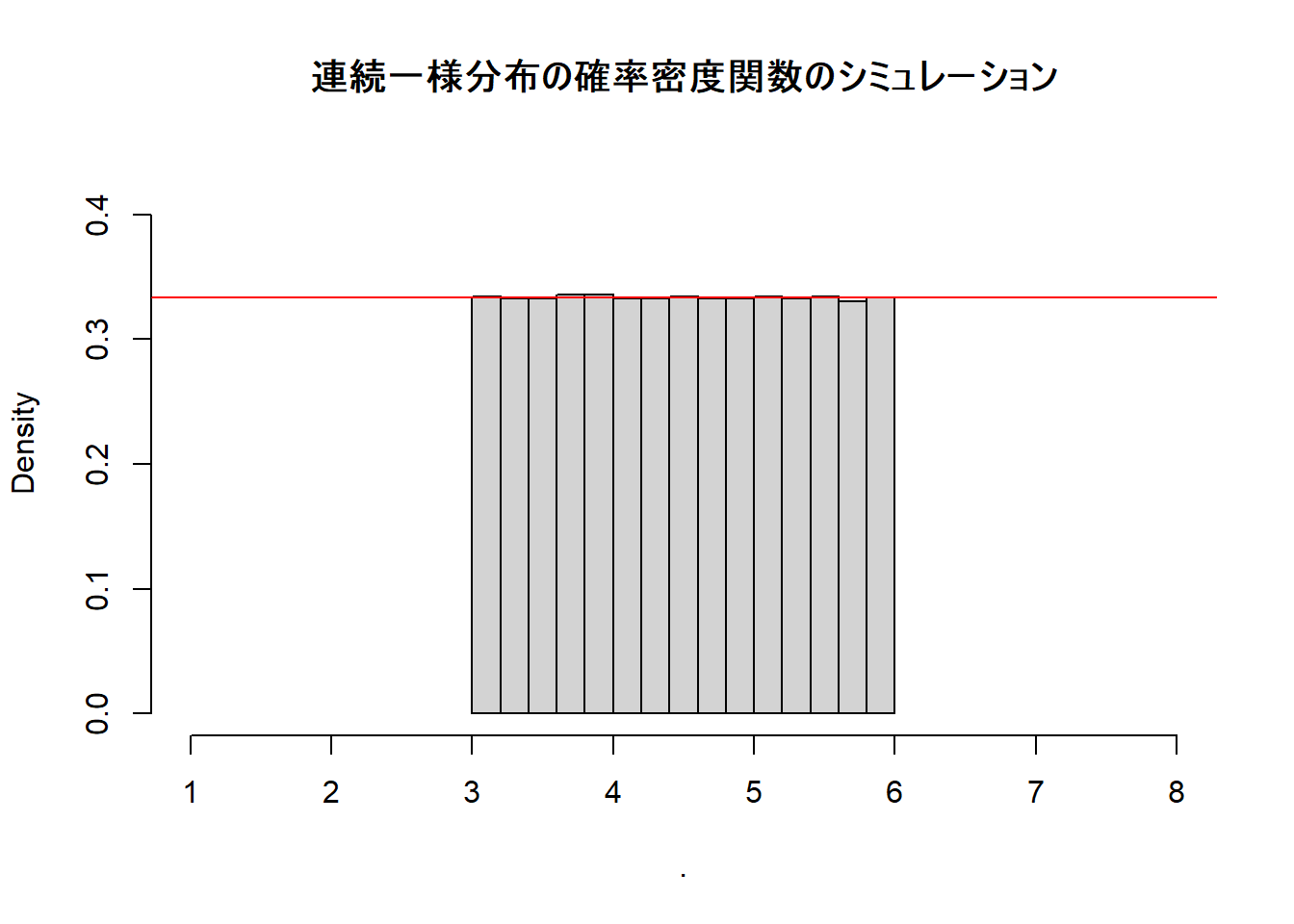
確率密度関数のシミュレーション
library(dplyr)
n <- 10^6
a <- 3
b <- 6
sample <- runif(n = n, min = a, max = b)
sample %>%
hist(xlim = c(a - 2, b + 2), ylim = c(0, h = 1 / (b - a) + 0.1), freq = F, main = "連続一様分布の確率密度関数のシミュレーション")
abline(h = 1 / (b - a), col = "red")
期待値の確認
sample %>% mean()
(a + b) / 2[1] 4.498834
[1] 4.5分散の確認
sample %>% var()
(b - a)^2 / 12[1] 0.7497179
[1] 0.75参考引用資料
