Rで粒子フィルタによる状態の推定と平滑化

こちらの続きです。

前回推定しました状態を 固定ラグ平滑化 により平滑化します。

「すべての履歴でなく、最近の \(L\) 個だけをリサンプルすると固定ラグ(\(L\) ラグ)平滑化が実現できる」
出典: http://www.mi.u-tokyo.ac.jp/mds-oudan/lecture_document_2019_math7/%E6%99%82%E7%B3%BB%E5%88%97%E8%A7%A3%E6%9E%90%EF%BC%8813%EF%BC%89_2019.pdf#page=29

「更にフィルタのアルゴリズムは、過去の履歴を記憶し、リサンプリングにおいて \(\mathbf{x}_{t|t-1}^{(i)}\) の代わりにベクトルを並べた量 \(\mathbf{z}_{t|t-1}^{(i)}=\left[\mathbf{x}_{t-L|t-1}^{(i)},\cdots,\mathbf{x}_{t-1|t-1}^{(i)},\mathbf{x}_{t|t-1}^{(i)}\right]\) を復元抽出することによって簡単に固定(\(L-\))ラグ平滑化に拡張できる」
出典: https://www.ieice.org/jpn/books/kaishikiji/2005/200512.pdf#page=4

Rコードはこちらの資料を参照引用しています。

http://www.mi.u-tokyo.ac.jp/mds-oudan/lecture_document_2019_math7/%E6%99%82%E7%B3%BB%E5%88%97%E8%A7%A3%E6%9E%90%EF%BC%8813%EF%BC%89_2019.pdf (以降、北川(2019))

北川(2019),p.31 中のコードのうちの平滑化に関するパート(以降、参照コード)の抜粋が以下の通りです。なお、参照コード68行目の lag+1:n は (lag+1):n に変更しています。

#####################
#
#  Particle smoother
#
model <- 1
m <- 10000
lag <- 20

# Gauss model
if (model == 1) {
  tau2 <- 0.018
  sig2 <- 1.045
  tau <- sqrt(tau2)
  sig <- sqrt(sig2)
}
# Cauchy model
if (model == "2") {
  tau22 <- 0.0000355
  sig22 <- 1.006
  scal2 <- sqrt(tau22)
  sig <- sqrt(sig22)
}


# Initial distribution
xf <- rnorm(m, mean = 0, sd = 1)
n <- length(y)
trend <- matrix(nrow = n, ncol = 7)
xs <- matrix(nrow = m, ncol = lag + 1)
# strend <- rep(0,length=n)
strend <- matrix(nrow = n, ncol = 7)

for (ii in 1:n) {
  #
  # Prediction step
  if (model == 1) {
    v <- rnorm(m, mean = 0, sd = tau)
  }
  if (model == 2) {
    v <- rcauchy(m, location = 0, scale = scal2)
  }

  xp <- xf + v

  # Bayes factor (weights of particles)
  alpha <- dnorm(y[ii] - xp, mean = 0, sd = sig, log = FALSE)
  alpha <- alpha / sum(alpha)

  # re-sampling
  # xf <- sample(xp,prob=alpha,replace=T)
  ind <- 1:m
  jnd <- sample(ind, prob = alpha, replace = T)
  for (i in 1:m) {
    xf[i] <- xp[jnd[i]]
    for (j in 1:lag) {
      xs[i, lag + 2 - j] <- xs[jnd[i], lag + 1 - j]
    }
    xs[i, 1] <- xf[i]
  }

  # trend[ii] <- mean(xf)
  # trend[ii,4] <- mean(xs[,lag+1])
  trend[ii, 3] <- quantile(xs[, lag + 1], prob = 0.1, na.rm = TRUE)
  trend[ii, 4] <- quantile(xs[, lag + 1], prob = 0.5, na.rm = TRUE)
  trend[ii, 5] <- quantile(xs[, lag + 1], prob = 0.9, na.rm = TRUE)
}

for (ii in (lag + 1):n) {
  strend[ii - lag, 4] <- trend[ii, 4]
  strend[ii - lag, 3] <- trend[ii, 3]
  strend[ii - lag, 5] <- trend[ii, 5]
}
for (ii in 1:lag) {
  # strend[n+1-ii,4] <- mean(xs[,ii])
  strend[n + 1 - ii, 3] <- quantile(xs[, ii], prob = 0.1, na.rm = TRUE)
  strend[n + 1 - ii, 4] <- quantile(xs[, ii], prob = 0.5, na.rm = TRUE)
  strend[n + 1 - ii, 5] <- quantile(xs[, ii], prob = 0.9, na.rm = TRUE)
}

49行目から59行目までが 固定ラグ平滑化 におけるリサンプリングのパートです。

参照コードでは xf は保管せずに時点が一つ移動する毎に上書きされていくため、同パートのループで行列変数 xs に、時点iiのウエイトでリサンプリングした粒子をラグの分だけ保存 しています。

Figure 1 は参考として 時点数(n) = 5、 粒子数(m) = 10、ラグ(j) = 5 とした場合に行列変数 xs にウエイトでリサンプリングされた粒子が保存されていく様子のアニメーションです。

ここで、ラグをどの程度取ることにするかの判断が必要になります。

「したがって、\(L\) はあまり大きくしないほうがよいことになる。通常は20程度、最大でも50以下にするほうがよい」
出典: https://www.ism.ac.jp/editsec/toukei/pdf/44-1-031.pdf#page=13

「このような問題を避けるために、一般に\(L\) を20から30程度に制限するか、次節で述べるようにリサンプル・ムーブ法を適用することが多い」
出典: https://www.jstage.jst.go.jp/article/jjssj/44/1/44_189/_pdf/-char/ja#page=14

本ページでは、北川(2019) にならってラグは 20 とします。

始めにサンプルデータを作成します。

コードは前回と同一です。但し、粒子数(m) は負荷軽減のため 1000 とし、配列にウエイト保管用 alpha を追記します。

library(tidyr)
library(ggplot2)
seed <- 20240617
set.seed(seed)
t <- rep(0, 400)
t[101:200] <- 1.5
t[201:300] <- -1
T <- length(t)
y <- rnorm(T, mean = t, sd = 1)
m <- 1000
xf <- rnorm(m, mean = 0, sd = 4)
log10tau2 <- runif(m, min = -8, max = -2)
w <- runif(m, min = sd(y) * 0.5, max = sd(y) * 2)
pfresult <- array(
  data = NA,
  dim = c(m, T, 4),
  dimnames = list(
    NULL,
    NULL,
    c("xf", "log10tau2", "w", "alpha")
  )
)
for (ii in seq(T)) {
  v <- rcauchy(n = m, location = 0, scale = sqrt(10^log10tau2))
  xp <- xf + v
  alpha <- dnorm(y[ii] - xp, mean = 0, sd = w) %>%
    {
      . / sum(.)
    }
  rs <- sample(seq(m), prob = alpha, replace = T)
  xf <- xp[rs]
  log10tau2 <- log10tau2[rs]
  w <- w[rs]
  pfresult[, ii, "xf"] <- xf
  pfresult[, ii, "log10tau2"] <- log10tau2
  pfresult[, ii, "w"] <- w
  pfresult[, ii, "alpha"] <- alpha
}
xf_mean <- apply(X = pfresult[, , "xf"], MARGIN = 2, FUN = function(x) mean(x))
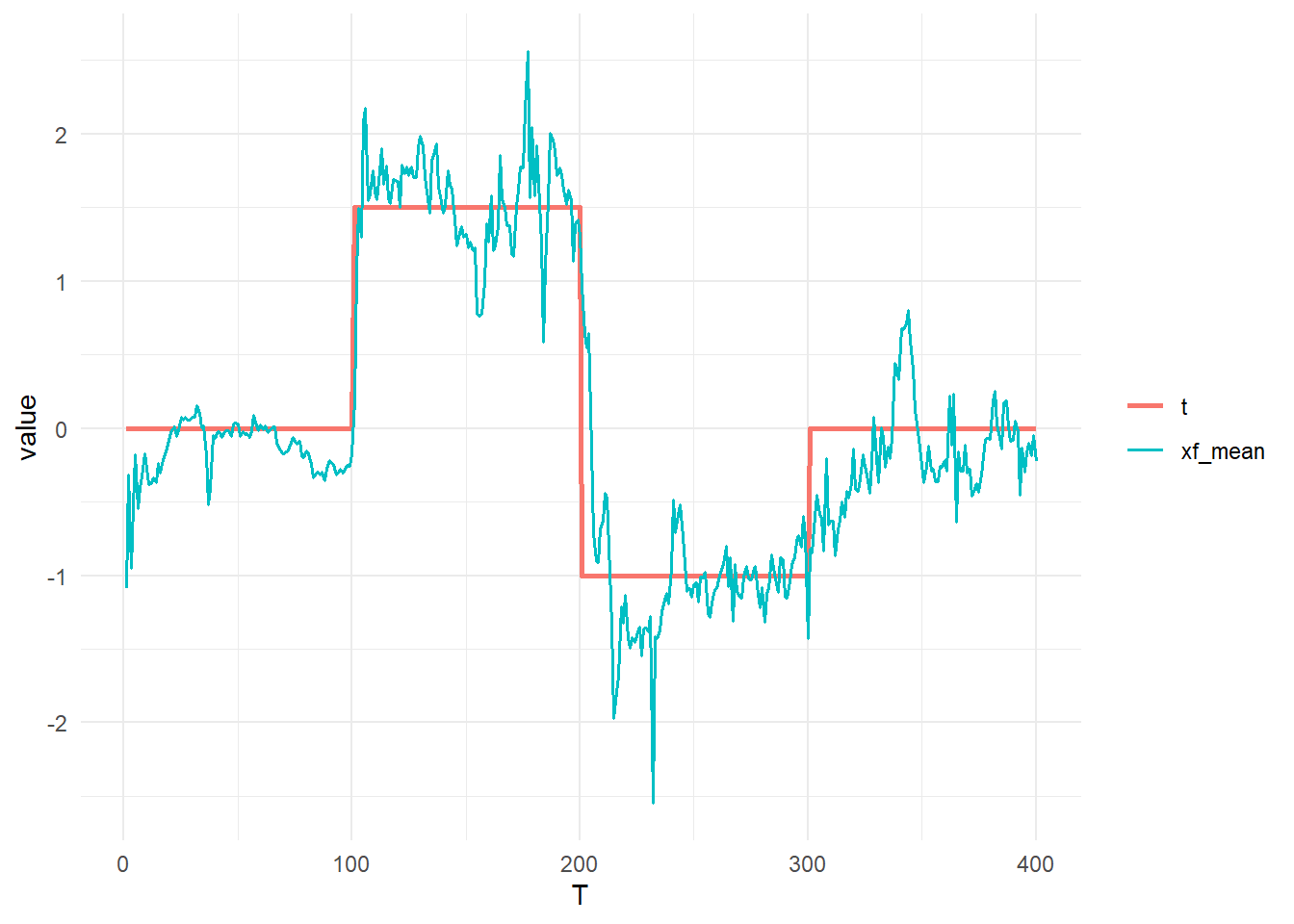
tidydf <- data.frame(T = seq(T), t, xf_mean) %>% gather(key = "key", value = "value", colnames(.)[-1])
ggplot() +
  geom_line(data = tidydf, aes(x = T, y = value, col = key, linewidth = key)) +
  theme_minimal() +
  scale_linewidth_manual(values = c(1.0, 0.7)) +
  theme(legend.title = element_blank())

固定ラグ平滑化を実行します。なお、本ページでは xf と alpha を配列に保存していますので、一つの時点の各粒子ごとに同時点のウエイトでラグ分のリサンプリングを行う参照コードとは異なり、配列を利用してまとめて平滑化する事とします。

set.seed(seed)
lag <- 20
xs <- matrix(data = NA, nrow = m * lag, T)
ii <- 1
for (ii in seq(T)) {
  rs <- pfresult[, ii, "alpha"] %>% sample(seq(m), prob = ., replace = T)
  target.columns <- tail(seq(ii), lag)
  xs <- pfresult[rs, target.columns, "xf"] %>%
    as.vector() %>%
    {
      xs[seq(.), ii] <- .
      xs
    }
}
xs_mean <- apply(X = xs, MARGIN = 2, FUN = function(x) na.omit(x) %>% mean())
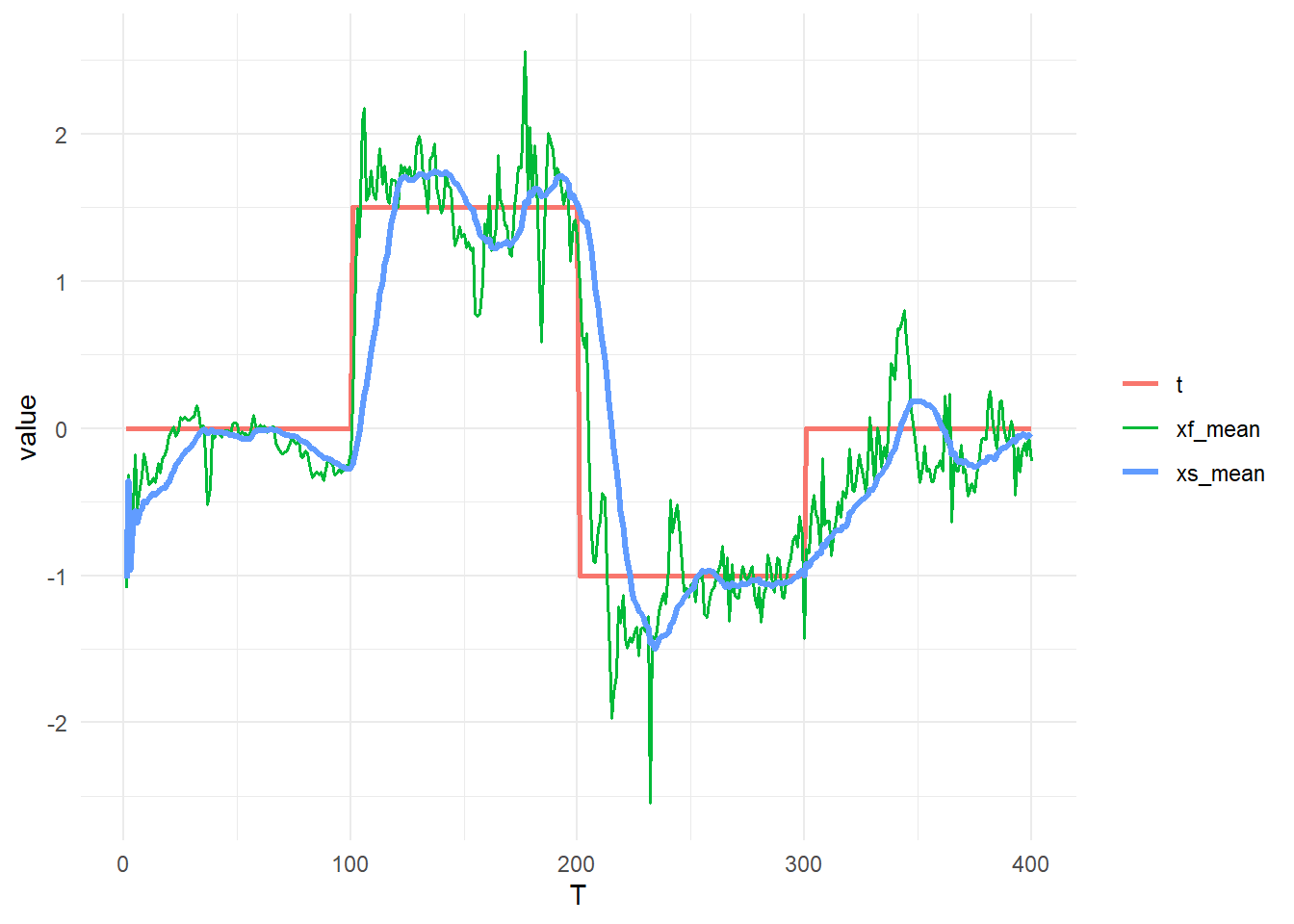
xs_quantile <- apply(X = xs, MARGIN = 2, FUN = function(x) na.omit(x) %>% quantile(probs = c(0.025, 0.975)))

状態(t)、平滑化前の推定(xf_mean)そして平滑化後の推定(xs_mean)を比較します。

tidydf <- data.frame(T = seq(T), t, xf_mean, xs_mean) %>% gather(key = "key", value = "value", colnames(.)[-1])
ggplot() +
  geom_line(data = tidydf, aes(x = T, y = value, col = key, linewidth = key)) +
  theme_minimal() +
  scale_linewidth_manual(values = c(1.0, 0.7, 1.2)) +
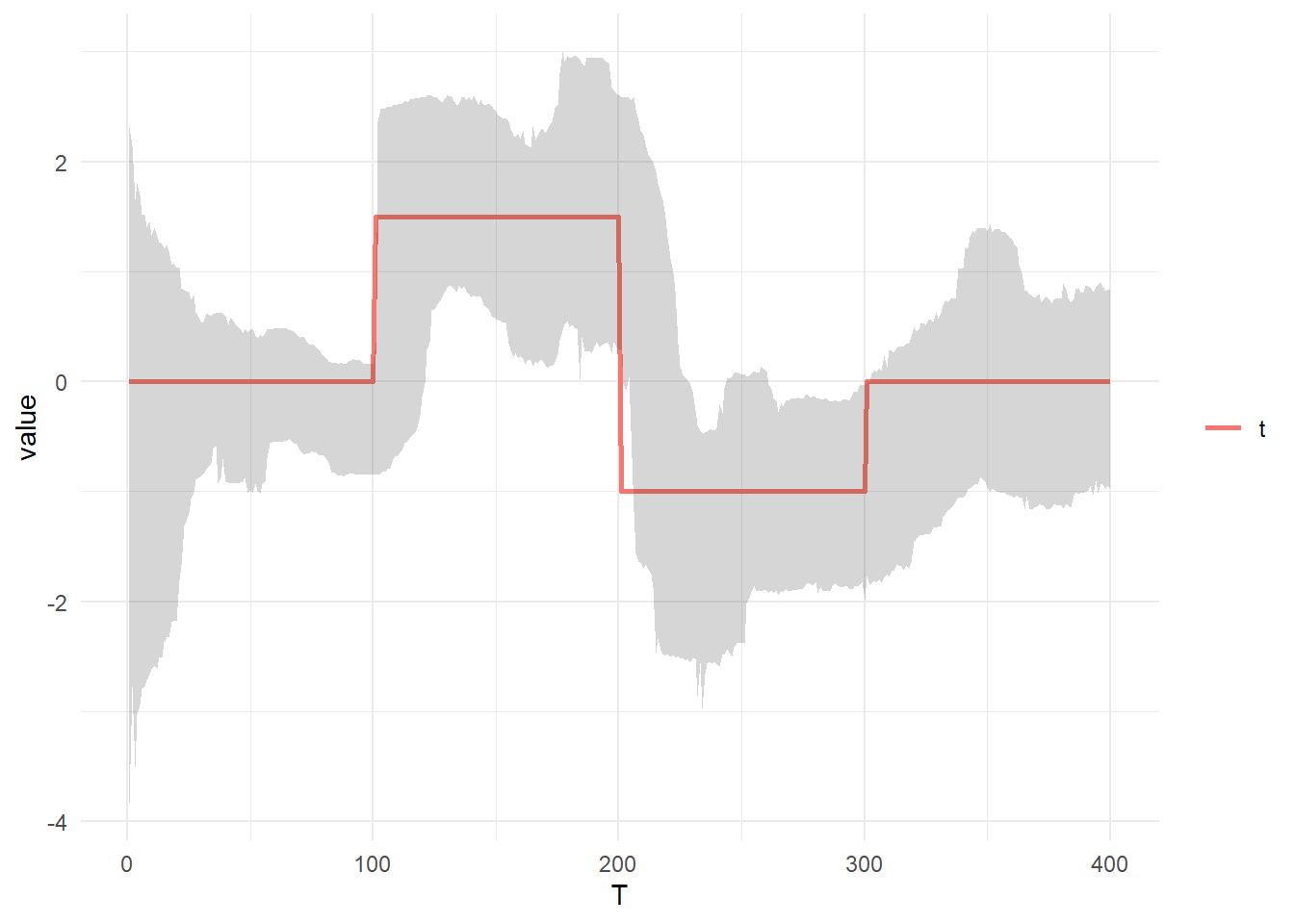
  theme(legend.title = element_blank())

状態(t)と平滑化後の 95%信用区間 を比較します。

tidydf <- data.frame(T = seq(T), t) %>% gather(key = "key", value = "value", colnames(.)[-1])
tidydf_ribbon <- t(xs_quantile) %>% data.frame(T = seq(T), ., check.names = F)
ggplot() +
  geom_line(data = tidydf, aes(x = T, y = value, col = key, linewidth = key)) +
  theme_minimal() +
  scale_linewidth_manual(values = 1.0) +
  theme(legend.title = element_blank()) +
  geom_ribbon(aes(x = tidydf_ribbon$T, ymin = tidydf_ribbon$`2.5%`, ymax = tidydf_ribbon$`97.5%`), alpha = 0.2)

以上です。