こちらの続きです。

線形モデルの残差平方和が、サンプルサイズから説明変数の個数を減じた結果を自由度としたカイ二乗分布に従うことをシミュレーションで確認します。
以降の数式、導出は https://stats.stackexchange.com/questions/20227/why-is-rss-distributed-chi-square-times-n-p?rq=1= を引用参照しています。
\(\mathbf{y}\left(n\times1\right)\)、\(\mathbf{X}\left(n\times k\right)\)、\(\boldsymbol{\beta}\left(k\times1\right)\)、\(\boldsymbol{\epsilon}\left(n\times 1\right)\) として次の線形モデルを考えます。 \[\mathbf{y} = \mathbf{X}\boldsymbol{\beta} + \boldsymbol{\epsilon}\] よって \[\begin{eqnarray}\hat{\boldsymbol{\epsilon}}=\mathbf{y}-\mathbf{X}\hat{\boldsymbol{\beta}}&=&\left(\mathbf{I}_n-\mathbf{X}\left(\mathbf{X}^\mathsf{T}\mathbf{X}\right)^{-1}\mathbf{X}^\mathsf{T}\right)\mathbf{y}\\&=&\mathbf{Py}\\&=&\mathbf{P}\left(\mathbf{X}\boldsymbol{\beta} + \boldsymbol{\epsilon}\right)\\&=&\mathbf{PX}\boldsymbol{\beta}+\mathbf{P}\boldsymbol{\epsilon}\tag{1}\end{eqnarray}\] ここで、\(\mathbf{P}=\mathbf{I}-\mathbf{X}\left(\mathbf{X}^\mathsf{T}\mathbf{X}\right)^{-1}\mathbf{X}^\mathsf{T}\) としています。
式(1)右辺第一項の \(\mathbf{P}\mathbf{X}\boldsymbol{\beta}\) は \[\begin{eqnarray}\mathbf{PX}\boldsymbol{\beta}&=&\left(\mathbf{I}-\mathbf{X}\left(\mathbf{X}^\mathsf{T}\mathbf{X}\right)^{-1}\mathbf{X}^\mathsf{T}\right)\mathbf{X}\boldsymbol{\beta}\\&=&\mathbf{X}\boldsymbol{\beta}-\mathbf{X}\left(\mathbf{X}^\mathsf{T}\mathbf{X}\right)^{-1}\mathbf{X}^\mathsf{T}\mathbf{X}\boldsymbol{\beta}\\&=&\mathbf{X}\boldsymbol{\beta}-\mathbf{X}\boldsymbol{\beta}\\&=&0\end{eqnarray}\] であるため \[\hat{\boldsymbol{\epsilon}}=\mathbf{P}\boldsymbol{\epsilon}\tag{2}\] となります。
また、\(\mathbf{P}\) は対称冪等行列であるため、そのトレースは \[\begin{eqnarray}\mathrm{tr}\left(\mathbf{P}\right)&=&\mathrm{tr}\left(\mathbf{I}-\mathbf{X}\left(\mathbf{X}^\mathsf{T}\mathbf{X}\right)^{-1}\mathbf{X}^\mathsf{T}\right)\\&=&\mathrm{rk}\left(\mathbf{I}-\mathbf{X}\left(\mathbf{X}^\mathsf{T}\mathbf{X}\right)^{-1}\mathbf{X}^\mathsf{T}\right)\\&=&\mathrm{rk}\left(\mathbf{I}\right)-\mathrm{rk}\left(\mathbf{X}\left(\mathbf{X}^\mathsf{T}\mathbf{X}\right)^{-1}\mathbf{X}^\mathsf{T}\right)\\&=&n-k\end{eqnarray}\] となり(参照資料: https://ymurasawa.web.fc2.com/ue-sl11.pdf)、その固有値は 0 か 1 となります(参照資料: https://ymurasawa.web.fc2.com/ue-sl10.pdf#page=11)。
サンプル \(\mathbf{P}(6\times6)\) で確認します。
サンプル \(\mathbf{P}\) の作成。
library(dplyr)
round.digits <- 10
seed.base <- 20240722
set.seed(seed.base)
n.sample <- 12
k <- 2
n <- n.sample/k
X <- rnorm(n = n.sample) %>% matrix(ncol = k)
P <- diag(n) - X %*% solve(t(X) %*% X) %*% t(X)
P [,1] [,2] [,3] [,4] [,5] [,6]
[1,] 0.939799330 -0.05582890 -0.2178170 -0.008583361 -0.04991379 0.05873983
[2,] -0.055828899 0.89435530 -0.2315147 -0.180297051 0.03128858 -0.06543667
[3,] -0.217817021 -0.23151474 0.1957265 -0.125480110 -0.13809221 0.14683196
[4,] -0.008583361 -0.18029705 -0.1254801 0.447449036 0.24106365 -0.37523427
[5,] -0.049913791 0.03128858 -0.1380922 0.241063646 0.84689676 0.22138459
[6,] 0.058739829 -0.06543667 0.1468320 -0.375234268 0.22138459 0.67577303冪等行列であることの確認 \(\mathbf{P}=\mathbf{P}\mathbf{P}\)
round(P,round.digits) == round(P %*% P,round.digits) [,1] [,2] [,3] [,4] [,5] [,6]
[1,] TRUE TRUE TRUE TRUE TRUE TRUE
[2,] TRUE TRUE TRUE TRUE TRUE TRUE
[3,] TRUE TRUE TRUE TRUE TRUE TRUE
[4,] TRUE TRUE TRUE TRUE TRUE TRUE
[5,] TRUE TRUE TRUE TRUE TRUE TRUE
[6,] TRUE TRUE TRUE TRUE TRUE TRUE固有値の確認。
eigen(P)$values %>% round(digits = round.digits)[1] 1 1 1 1 0 0トレース(ランク) \(n-k=\) 4 の確認。
qr(P)$rank[1] 4さらに、実対称行列は直交行列によって対角化可能であるため(参照資料: https://risalc.info/src/real-symmetric-matrix.html#dia、https://en.wikipedia.org/wiki/Diagonalizable_matrix#Examples)、\[\mathbf{V}^\mathsf{T}\mathbf{P}\mathbf{V}=\boldsymbol{\Lambda}\] を満たす対角行列 \(\boldsymbol{\Lambda}=\begin{bmatrix}\mathbf{I}_{n-k}&\mathbf{0}\\\mathbf{0}&\mathbf{0}\end{bmatrix}\) と直交行列 \(\mathbf{V}\) が存在します。
「ユニタリ行列 \(\mathbf{U}_\mathrm{U}\) のすべての成分が実数であるならば,これは,直交行列 \(\mathbf{U}\) に他ならない」
出典: https://mathema.jp/wp-content/uploads/2023/08/3d5b5e41ef969c16b7ab736807440acf.pdf#page=6
「直交行列 \(\mathbf{R}\) の逆行列は 転置行列である」
出典: https://risalc.info/src/orthogonal-matrix-properties.html#inv
\(\mathbf{X}(6\times 2)\) としたサンプルで確認します。
library(dplyr)
set.seed(seed.base)
n <- 12
n.col <- 2
X <- rnorm(n = n) %>% matrix(ncol = n.col)
P <- diag(n / n.col) - X %*% solve(t(X) %*% X) %*% t(X)
list(P = P, X = X, XXT = X %*% t(X))$P
[,1] [,2] [,3] [,4] [,5] [,6]
[1,] 0.939799330 -0.05582890 -0.2178170 -0.008583361 -0.04991379 0.05873983
[2,] -0.055828899 0.89435530 -0.2315147 -0.180297051 0.03128858 -0.06543667
[3,] -0.217817021 -0.23151474 0.1957265 -0.125480110 -0.13809221 0.14683196
[4,] -0.008583361 -0.18029705 -0.1254801 0.447449036 0.24106365 -0.37523427
[5,] -0.049913791 0.03128858 -0.1380922 0.241063646 0.84689676 0.22138459
[6,] 0.058739829 -0.06543667 0.1468320 -0.375234268 0.22138459 0.67577303
$X
[,1] [,2]
[1,] -0.1225418 0.27494495
[2,] -0.5952908 -0.01699499
[3,] -0.7072751 0.84578604
[4,] -1.5583226 -0.83087486
[5,] 0.5920127 0.61962878
[6,] -0.9525443 -0.87366570
$XXT
[,1] [,2] [,3] [,4] [,5] [,6]
[1,] 0.09061123 0.06827535 0.31921540 -0.03748511 0.09781747 -0.12348344
[2,] 0.06827535 0.35466001 0.40666026 0.94177589 -0.36295033 0.58188881
[3,] 0.31921540 0.40666026 1.21559208 0.39942043 0.10535752 -0.06522342
[4,] -0.03748511 0.94177589 0.39942043 3.11872243 -1.43738079 2.21027814
[5,] 0.09781747 -0.36295033 0.10535752 -1.43738079 0.73441889 -1.10526674
[6,] -0.12348344 0.58188881 -0.06522342 2.21027814 -1.10526674 1.67063234\(\mathbf{P}\) が対称行列であるか確認します。
round(P, round.digits) == round(t(P), round.digits) [,1] [,2] [,3] [,4] [,5] [,6]
[1,] TRUE TRUE TRUE TRUE TRUE TRUE
[2,] TRUE TRUE TRUE TRUE TRUE TRUE
[3,] TRUE TRUE TRUE TRUE TRUE TRUE
[4,] TRUE TRUE TRUE TRUE TRUE TRUE
[5,] TRUE TRUE TRUE TRUE TRUE TRUE
[6,] TRUE TRUE TRUE TRUE TRUE TRUE\(\mathbf{P}\) が冪等行列であるか確認します。
round(P, round.digits) == round(P %*% P, round.digits) [,1] [,2] [,3] [,4] [,5] [,6]
[1,] TRUE TRUE TRUE TRUE TRUE TRUE
[2,] TRUE TRUE TRUE TRUE TRUE TRUE
[3,] TRUE TRUE TRUE TRUE TRUE TRUE
[4,] TRUE TRUE TRUE TRUE TRUE TRUE
[5,] TRUE TRUE TRUE TRUE TRUE TRUE
[6,] TRUE TRUE TRUE TRUE TRUE TRUE\(\mathbf{P}\) の固有値が 0 か 1 であることを確認します。
eigen(P)$values %>% round(round.digits)[1] 1 1 1 1 0 0\(\mathbf{P}\) の固有ベクトルを確認します。
V <- eigen(P)$vectors
V [,1] [,2] [,3] [,4] [,5] [,6]
[1,] 0.68204190 0.00000000 0.0000000 0.68892538 -0.208611838 -0.12915793
[2,] -0.70370408 0.08579823 -0.1130829 0.61563527 -0.315640810 0.07756017
[3,] -0.00528651 -0.13775225 0.2829169 -0.31093556 -0.821737615 -0.35919457
[4,] 0.19208058 0.15225563 -0.5884873 -0.20262044 -0.420607191 0.61289522
[5,] 0.01352995 0.90516861 -0.1414704 -0.08584643 0.002982498 -0.39127273
[6,] 0.05013450 0.36214776 0.7354176 0.03562941 -0.068410291 0.56528489\(\mathbf{V}\) が直交行列であるか確認します。
t(V) %*% V %>% round(round.digits) [,1] [,2] [,3] [,4] [,5] [,6]
[1,] 1 0 0 0 0 0
[2,] 0 1 0 0 0 0
[3,] 0 0 1 0 0 0
[4,] 0 0 0 1 0 0
[5,] 0 0 0 0 1 0
[6,] 0 0 0 0 0 1\(\mathbf{V}^{-1}\mathbf{P}\mathbf{V}\) が \(\begin{bmatrix}\mathbf{I}_{6-2=4}&\mathbf{0}\\\mathbf{0}&\mathbf{0}\end{bmatrix}\) となるか確認します。
solve(V) %*% P %*% V %>% round(round.digits) [,1] [,2] [,3] [,4] [,5] [,6]
[1,] 1 0 0 0 0 0
[2,] 0 1 0 0 0 0
[3,] 0 0 1 0 0 0
[4,] 0 0 0 1 0 0
[5,] 0 0 0 0 0 0
[6,] 0 0 0 0 0 0同じく \(\mathbf{V}^\mathsf{T}\mathbf{P}\mathbf{V}\) を確認します。
t(V) %*% P %*% V %>% round(round.digits) [,1] [,2] [,3] [,4] [,5] [,6]
[1,] 1 0 0 0 0 0
[2,] 0 1 0 0 0 0
[3,] 0 0 1 0 0 0
[4,] 0 0 0 1 0 0
[5,] 0 0 0 0 0 0
[6,] 0 0 0 0 0 0ここで、\(\boldsymbol{\epsilon}\sim \mathrm{N}\left(0,\sigma^2\right)\) とすると、式(2)の通り \(\hat{\boldsymbol{\epsilon}}=\mathbf{Q}\epsilon\) であるので \[\hat{\boldsymbol{\epsilon}}\sim \mathrm{N}\left(0,\sigma^2\mathbf{Q}\right)\] となり、\(\mathrm{E}\left(\hat{\boldsymbol{\epsilon}}\right)=0\) であるため \(\mathbf{K}=\mathbf{V}^\mathsf{T}\hat{\boldsymbol{\epsilon}}\) とすると \[\begin{eqnarray}\mathrm{cov}\left(\mathbf{k}\right)=\mathrm{cov}\left(\mathbf{V}^\mathsf{T}\hat{\boldsymbol{\epsilon}}\right)&=&\mathrm{E}\left(\left(\mathbf{V}^\mathsf{T}\hat{\boldsymbol{\epsilon}}-\mathbf{V}^\mathsf{T}\mathrm{E}\left(\hat{\boldsymbol{\epsilon}}\right)\right)\left(\mathbf{V}^\mathsf{T}\hat{\boldsymbol{\epsilon}}-\mathbf{V}^\mathsf{T}\mathrm{E}\left(\hat{\boldsymbol{\epsilon}}\right)\right)^\mathsf{T}\right)\\&=&\mathrm{E}\left(\mathbf{V}^\mathsf{T}\left(\hat{\boldsymbol{\epsilon}}-\mathrm{E}\left(\hat{\boldsymbol{\epsilon}}\right)\right)\left(\hat{\boldsymbol{\epsilon}}-\mathrm{E}\left(\hat{\boldsymbol{\epsilon}}\right)\right)^\mathsf{T}\mathbf{V}\right)\\&=&\mathbf{V}^\mathsf{T}\mathrm{E}\left(\left(\hat{\boldsymbol{\epsilon}}-\mathrm{E}\left(\hat{\boldsymbol{\epsilon}}\right)\right)\left(\hat{\boldsymbol{\epsilon}}-\mathrm{E}\left(\hat{\boldsymbol{\epsilon}}\right)\right)^\mathsf{T}\right)\mathbf{V}\\&=&\mathbf{V}^\mathsf{T}\mathrm{cov}\left(\hat{\boldsymbol{\epsilon}}\right)\mathbf{V}\\&=&\sigma^2\mathbf{V}^\mathsf{T}\mathbf{Q}\mathbf{V}\\&=&\sigma^2\boldsymbol{\Lambda}\end{eqnarray}\] と展開され \[\mathbf{k}\sim\mathrm{N}\left(0,\sigma^2\boldsymbol{\Lambda}\right)\] となります。
よって \[k_{n-k+1}=\cdots=k_n=0\] となるため \[\mathbf{k}^{*}=\left(k_1,\cdots k_{n-k}\right)^\mathsf{T}\] とすると \[\dfrac{\|\mathbf{k}\|^2}{\sigma^2}=\dfrac{\|\mathbf{k}^{*}\|^2}{\sigma^2}\] となります。
さらに \[\dfrac{\|\mathbf{k}^{*}\|^2}{\sigma^2}\sim\chi^2_{n-k}\] であるため \[\dfrac{\|\mathbf{k}\|^2}{\sigma^2}\sim\chi^2_{n-k}\] といえます。
また、\(\mathbf{V}\) が直交行列であるためノルムは変化せず(参照資料: https://risalc.info/src/orthogonal-matrix-properties.html#norm) \[\|\mathbf{k}\|^2=\|\mathbf{V}\hat{\boldsymbol{\epsilon}}\|^2=\|\hat{\boldsymbol{\epsilon}}\|^2\] となり、よって \[\dfrac{\hat{\boldsymbol{\epsilon}}^\mathsf{T}\hat{\boldsymbol{\epsilon}}}{\sigma^2}\sim\chi^2_{n-k}\] となります。
続いて、\(\mathbf{y}\left(n\times1\right),\,\mathbf{X}\left(n\times k\right),\,\boldsymbol{\beta}\left(k\times1\right),\,\boldsymbol{\epsilon}\left(n\times 1\right)\) とした線形モデルを考え、\(\dfrac{\hat{\boldsymbol{\epsilon}}^\mathsf{T}\hat{\boldsymbol{\epsilon}}}{\sigma^2}\) の分布を確認します。
試行回数を 10,000回 とし \(k=10,\,n=200\)、そして真の分散を \(\sigma^2=5\) として、10,000個 の \(\dfrac{\hat{\boldsymbol{\epsilon}}^\mathsf{T}\hat{\boldsymbol{\epsilon}}}{\sigma^2}\) を作成します。
k <- 10
n <- 200
iteration <- 10000
test.stat <- vector()
true.sigma2 <- 5
for (iii in seq(iteration)) {
set.seed(seed.base + iii)
X <- rnorm(n = k * n, mean = 0, sd = 1) %>% matrix(nrow = n)
X[, 1] <- 1
beta <- rnorm(n = k) %>% matrix(ncol = 1)
e <- rnorm(n = n, mean = 0, sd = true.sigma2^0.5) %>% matrix(ncol = 1)
y <- X %*% beta + e
hat.beta <- solve(t(X) %*% X) %*% t(X) %*% y
hat.e <- y - X %*% hat.beta
test.stat[iii] <- (t(hat.e) %*% hat.e) / true.sigma2
}
summarytools::descr(test.stat)Descriptive Statistics
test.stat
N: 10000
test.stat
----------------- -----------
Mean 190.23
Std.Dev 19.51
Min 132.53
Q1 176.86
Median 189.19
Q3 202.95
Max 265.22
MAD 19.31
IQR 26.09
CV 0.10
Skewness 0.24
SE.Skewness 0.02
Kurtosis 0.00
N.Valid 10000.00
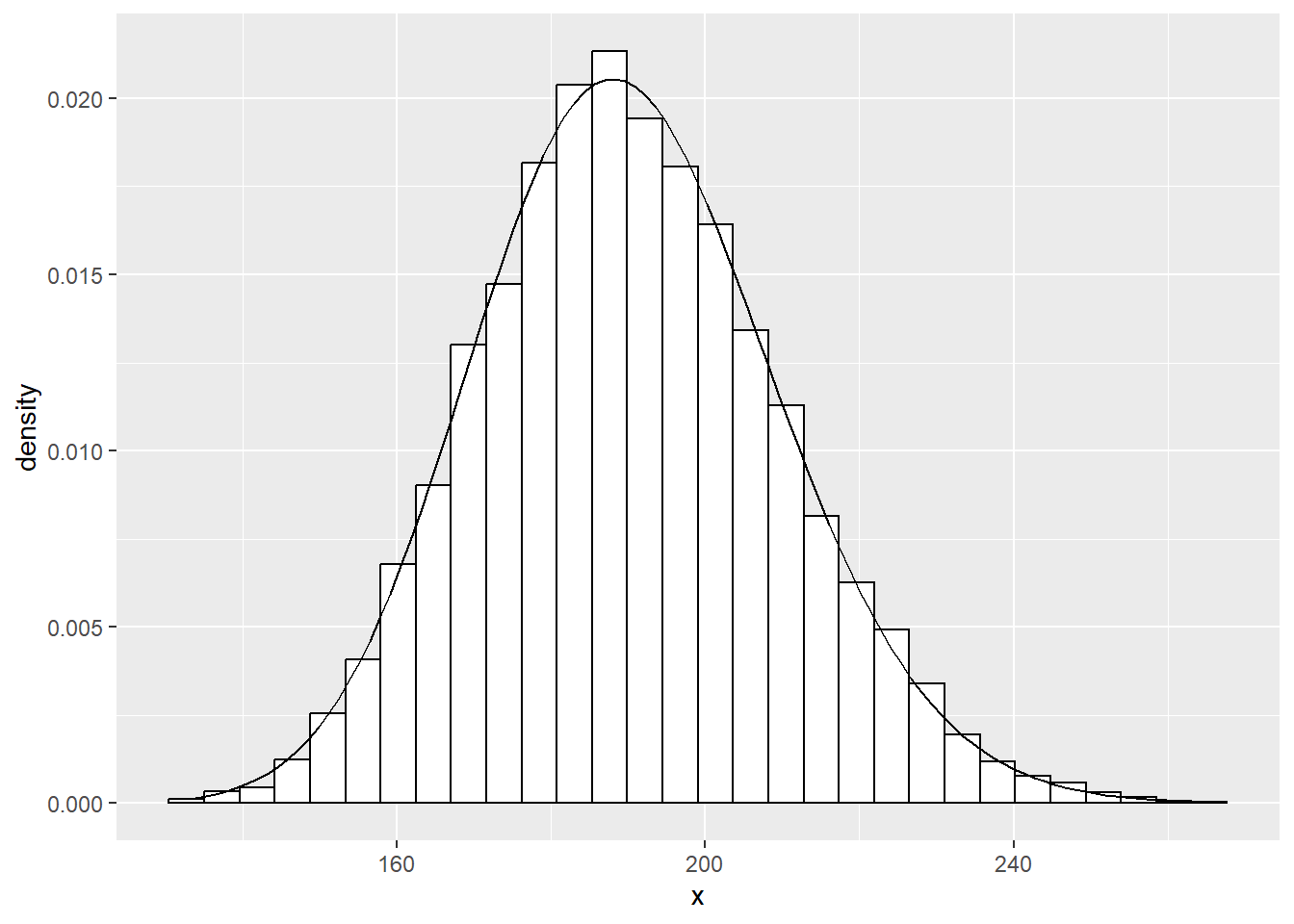
Pct.Valid 100.00シミュレーションの結果( test.stat ) のヒストグラムと 自由度 190(= n - k) のカイ二乗分布を重ね合わせて確認します。
library(ggplot2)
df <- data.frame(x = test.stat)
ggplot(df, aes(x = x)) +
geom_histogram(aes(y = after_stat(density)),
colour = "black",
fill = "white"
) +
stat_function(fun = dchisq, args = list(df = n - k, ncp = 0), geom = "line")`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.誤差分散の不偏推定量は \[\hat{\sigma}^2=\dfrac{\hat{\boldsymbol{\epsilon}}^\mathsf{T}\hat{\boldsymbol{\epsilon}}}{n-k}\] であるため \[\dfrac{\hat{\boldsymbol{\epsilon}}^\mathsf{T}\hat{\boldsymbol{\epsilon}}}{\sigma^2}=\dfrac{(n-k)\,\hat{\sigma}^2}{\sigma^2}\] も結果は同じです。
k <- 10
n <- 200
iteration <- 10000
test.stat1 <- test.stat2 <- vector()
true.sigma2 <- 5
for (iii in seq(iteration)) {
set.seed(seed.base + iii)
X <- rnorm(n = k * n, mean = 0, sd = 1) %>% matrix(nrow = n)
X[, 1] <- 1
beta <- rnorm(n = k) %>% matrix(ncol = 1)
e <- rnorm(n = n, mean = 0, sd = true.sigma2^0.5) %>% matrix(ncol = 1)
y <- X %*% beta + e
hat.beta <- solve(t(X) %*% X) %*% t(X) %*% y
hat.e <- y - X %*% hat.beta
test.stat1[iii] <- (t(hat.e) %*% hat.e) / true.sigma2
hat.sigma2 <- (t(hat.e - mean(hat.e)) %*% (hat.e - mean(hat.e))) / (n - k)
test.stat2[iii] <- (n - k) * hat.sigma2 / true.sigma2
}
summarytools::descr(data.frame(test.stat1, test.stat2))Descriptive Statistics
test.stat1 test.stat2
----------------- ------------ ------------
Mean 190.23 190.23
Std.Dev 19.51 19.51
Min 132.53 132.53
Q1 176.86 176.86
Median 189.19 189.19
Q3 202.95 202.95
Max 265.22 265.22
MAD 19.31 19.31
IQR 26.09 26.09
CV 0.10 0.10
Skewness 0.24 0.24
SE.Skewness 0.02 0.02
Kurtosis 0.00 0.00
N.Valid 10000.00 10000.00
Pct.Valid 100.00 100.00以上です。