こちらの続きです。

以降の数式、導出は https://qiita.com/ykawakubo/items/327dbdb0379f87aa9248 を参照引用しています。
OLS推定量 \(\hat{\boldsymbol{\beta}}\) の部分ベクトル \(\hat{\boldsymbol{\beta}_2}\) は \(\tilde{\boldsymbol{\beta}}_2\) (残差回帰推定量)と一致するため、 \[\begin{eqnarray}\hat{\boldsymbol{\beta}}_2=\tilde{\boldsymbol{\beta}}_2&=&\left(\tilde{\mathbf{X}}_2^\mathsf{T}\tilde{\mathbf{X}}_2\right)^{-1} \tilde{\mathbf{X}}_2^\mathsf{T} \tilde{y}\\&=&\left(\tilde{\mathbf{X}}_2^\mathsf{T}\tilde{\mathbf{X}}_2\right)^{-1} \tilde{\mathbf{X}}_2^\mathsf{T}\left(\mathbf{I}_n-\mathbf{P}_1\right)y\\&=&\left(\tilde{\mathbf{X}}_2^\mathsf{T}\tilde{\mathbf{X}}_2\right)^{-1} \tilde{\mathbf{X}}_2^\mathsf{T}\left(\mathbf{I}_n-\mathbf{P}_1\right)\left(\mathbf{X}_1\boldsymbol{\beta}_1+\mathbf{X}_2\boldsymbol{\beta}_2+\boldsymbol{\epsilon}\right)\end{eqnarray}\] となり、ここで \[\begin{eqnarray}\left(\mathbf{I}_n-\mathbf{P}_1\right)\mathbf{X}_1&=&\mathbf{I}_n\mathbf{X}_1-\mathbf{P}_1\mathbf{X}_1\\&=&\mathbf{X}_1-\mathbf{X}_1\left(\mathbf{X}_1^{\mathsf{T}}\mathbf{X}_1\right)^{-1}\mathbf{X}_1^{\mathsf{T}}\mathbf{X}_1\\&=&\mathbf{X}_1-\mathbf{X}_1\mathbf{I}_n\\&=&0\end{eqnarray}\] であることから \(\hat{\boldsymbol{\beta}}_2\) は以下の通りに展開できる。 \[\begin{eqnarray}\hat{\boldsymbol{\beta}}_2=\tilde{\boldsymbol{\beta}}_2&=&\left(\tilde{\mathbf{X}}_2^\mathsf{T}\tilde{\mathbf{X}}_2\right)^{-1}\tilde{\mathbf{X}}_2^\mathsf{T}\tilde{\mathbf{y}}\\&=&\left(\tilde{\mathbf{X}}_2^\mathsf{T}\tilde{\mathbf{X}}_2\right)^{-1}\tilde{\mathbf{X}}_2^\mathsf{T}\left(\mathbf{I}_n-\mathbf{P}_1\right)\mathbf{y}\\&=&\left(\tilde{\mathbf{X}}_2^\mathsf{T}\tilde{\mathbf{X}}_2\right)^{-1} \tilde{\mathbf{X}}_2^\mathsf{T}\left(\mathbf{I}_n-\mathbf{P}_1\right)\left(\mathbf{X}_1\boldsymbol{\beta}_1+\mathbf{X}_2\boldsymbol{\beta}_2+\boldsymbol{\epsilon}\right)\\&=&\left(\tilde{\mathbf{X}}_2^\mathsf{T}\tilde{\mathbf{X}}_2\right)^{-1} \tilde{\mathbf{X}}_2^\mathsf{T}\left(\mathbf{I}_n-\mathbf{P}_1\right)\left(\mathbf{X}_2\boldsymbol{\beta}_2+\boldsymbol{\epsilon}\right)\\&=&\left(\tilde{\mathbf{X}}_2^\mathsf{T}\tilde{\mathbf{X}}_2\right)^{-1} \tilde{\mathbf{X}}_2^\mathsf{T}\left(\mathbf{I}_n-\mathbf{P}_1\right)\mathbf{X}_2\boldsymbol{\beta}_2+\left(\tilde{\mathbf{X}}_2^\mathsf{T}\tilde{\mathbf{X}}_2\right)^{-1} \tilde{\mathbf{X}}_2^\mathsf{T}\left(\mathbf{I}_n-\mathbf{P}_1\right)\boldsymbol{\epsilon}\\&=&\left(\tilde{\mathbf{X}}_2^\mathsf{T}\tilde{\mathbf{X}}_2\right)^{-1} \tilde{\mathbf{X}}_2^\mathsf{T}\tilde{\mathbf{X}}_2\boldsymbol{\beta}_2+\left(\tilde{\mathbf{X}}_2^\mathsf{T}\tilde{\mathbf{X}}_2\right)^{-1} \tilde{\mathbf{X}}_2^\mathsf{T}\left(\mathbf{I}_n-\mathbf{P}_1\right)\boldsymbol{\epsilon}\\&=&\mathbf{I}_n\boldsymbol{\beta}_2+\left(\tilde{\mathbf{X}}_2^\mathsf{T}\tilde{\mathbf{X}}_2\right)^{-1} \tilde{\mathbf{X}}_2^\mathsf{T}\left(\mathbf{I}_n-\mathbf{P}_1\right)\boldsymbol{\epsilon}\\&=&\boldsymbol{\beta}_2+\left(\tilde{\mathbf{X}}_2^\mathsf{T}\tilde{\mathbf{X}}_2\right)^{-1} \tilde{\mathbf{X}}_2^\mathsf{T}\left(\mathbf{I}_n-\mathbf{P}_1\right)\boldsymbol{\epsilon}\tag{1}\end{eqnarray}\] さらに、\(\mathbf{I}_n-\mathbf{P}_1\) が対称行列であることから \(\tilde{\mathbf{X}}_2^\mathsf{T}\) と \(\mathbf{X}_2^\mathsf{T}\) はそれぞれ \[\begin{eqnarray}\tilde{\mathbf{X}}_2&=&\left(\mathbf{I}_n-\mathbf{P}_1\right)\mathbf{X}_2\\&=&\left(\mathbf{I}_n-\mathbf{P}_1\right)^\mathsf{T}\mathbf{X}_2\\\tilde{\mathbf{X}}_2^\mathsf{T}&=&\mathbf{X}_2^\mathsf{T}\left(\mathbf{I}_n-\mathbf{P}_1\right)\end{eqnarray}\] と \[\begin{eqnarray}\tilde{\mathbf{X}}_2&=&\left(\mathbf{I}_n-\mathbf{P}_1\right)\mathbf{X}_2\\\left(\mathbf{I}_n-\mathbf{P}_1\right)^{-1}\tilde{\mathbf{X}}_2&=&\mathbf{X}_2\\\tilde{\mathbf{X}}_2^\mathsf{T}\left(\left(\mathbf{I}_n-\mathbf{P}_1\right)^{-1}\right)^\mathsf{T}&=&\mathbf{X}_2^\mathsf{T}\\\tilde{\mathbf{X}}_2^\mathsf{T}\left(\left(\mathbf{I}_n-\mathbf{P}_1\right)^{\mathsf{T}}\right)^\mathsf{-1}&=&\mathbf{X}_2^\mathsf{T}\\\tilde{\mathbf{X}}_2^\mathsf{T}\left(\mathbf{I}_n-\mathbf{P}_1\right)^\mathsf{-1}&=&\mathbf{X}_2^\mathsf{T}\end{eqnarray}\] とに表すことが出来る。
併せて \(\left(\mathbf{I}_n-\mathbf{P}_1\right)\) は冪等行列であることを利用すると、式(1)の右辺第二項は \[\begin{eqnarray}\left(\tilde{\mathbf{X}}_2^\mathsf{T}\tilde{\mathbf{X}}_2\right)^{-1} \tilde{\mathbf{X}}_2^\mathsf{T}\left(\mathbf{I}_n-\mathbf{P}_1\right)\boldsymbol{\epsilon}&=&\left(\tilde{\mathbf{X}}_2^\mathsf{T}\tilde{\mathbf{X}}_2\right)^{-1} \mathbf{X}_2^\mathsf{T}\left(\mathbf{I}_n-\mathbf{P}_1\right)\left(\mathbf{I}_n-\mathbf{P}_1\right)\boldsymbol{\epsilon}\\&=&\left(\tilde{\mathbf{X}}_2^\mathsf{T}\tilde{\mathbf{X}}_2\right)^{-1} \mathbf{X}_2^\mathsf{T}\left(\mathbf{I}_n-\mathbf{P}_1\right)\boldsymbol{\epsilon}\\&=&\left(\tilde{\mathbf{X}}_2^\mathsf{T}\tilde{\mathbf{X}}_2\right)^{-1} \tilde{\mathbf{X}}_2^\mathsf{T}\left(\mathbf{I}_n-\mathbf{P}_1\right)^{-1}\left(\mathbf{I}_n-\mathbf{P}_1\right)\boldsymbol{\epsilon}\\&=&\left(\tilde{\mathbf{X}}_2^\mathsf{T}\tilde{\mathbf{X}}_2\right)^{-1} \tilde{\mathbf{X}}_2^\mathsf{T}\boldsymbol{\epsilon}\end{eqnarray}\] と展開できるため \(\hat{\boldsymbol{\beta}}_2\) は \[\hat{\boldsymbol{\beta}}_2=\boldsymbol{\beta}_2+\left(\tilde{\mathbf{X}}_2^\mathsf{T}\tilde{\mathbf{X}}_2\right)^{-1} \tilde{\mathbf{X}}_2^\mathsf{T}\boldsymbol{\epsilon}\tag{2}\] となり \(\mathrm{E}\left(\epsilon\right)=0\) であるため \(\mathrm{E}\left(\hat{\boldsymbol{\beta}}_2\right)=\boldsymbol{\beta}_2\tag{2}\) となる。
さらに \(\hat{\boldsymbol{\beta}}_2\) の分散共分散行列は \[\mathrm{var}\left(\hat{\boldsymbol{\beta}}_2\right)=\mathrm{cov}\left(\hat{\boldsymbol{\beta}}_2\right) =\Sigma=\mathrm{E}\left(\left(\hat{\boldsymbol{\beta}}_2-\boldsymbol{\beta}_2\right)\left(\hat{\boldsymbol{\beta}}_2-\boldsymbol{\beta}_2\right)^\mathsf{T}\right)\] となるが、式(2)より \[\hat{\boldsymbol{\beta}}_2-\boldsymbol{\beta}_2=\boldsymbol{\beta}_2+\left(\tilde{\mathbf{X}}_2^\mathsf{T}\tilde{\mathbf{X}}_2\right)^{-1} \tilde{\mathbf{X}}_2^\mathsf{T}\boldsymbol{\epsilon}-\boldsymbol{\beta}_2=\left(\tilde{\mathbf{X}}_2^\mathsf{T}\tilde{\mathbf{X}}_2\right)^{-1} \tilde{\mathbf{X}}_2^\mathsf{T}\boldsymbol{\epsilon}\] であり、さらに \[\mathrm{E}\left(\boldsymbol{\epsilon}\boldsymbol{\epsilon}^\mathsf{T}\right)=\sigma^2\mathbf{I}_n\] とすると \[\begin{eqnarray}\mathrm{E}\left(\left(\hat{\boldsymbol{\beta}}_2-\boldsymbol{\beta}_2\right)\left(\hat{\boldsymbol{\beta}}_2-\boldsymbol{\beta}_2\right)^\mathsf{T}\right)&=&\left(\tilde{\mathbf{X}}_2^\mathsf{T}\tilde{\mathbf{X}}_2\right)^{-1} \tilde{\mathbf{X}}_2^\mathsf{T}\mathrm{E}\left(\boldsymbol{\epsilon}\boldsymbol{\epsilon}^\mathsf{T}\right)\tilde{\mathbf{X}}_2\left(\tilde{\mathbf{X}}_2^\mathsf{T}\tilde{\mathbf{X}}_2\right)^{-1}\\&=&\sigma^2\left(\tilde{\mathbf{X}}_2^\mathsf{T}\tilde{\mathbf{X}}_2\right)^{-1} \tilde{\mathbf{X}}_2^\mathsf{T}\tilde{\mathbf{X}}_2\left(\tilde{\mathbf{X}}_2^\mathsf{T}\tilde{\mathbf{X}}_2\right)^{-1}\\&=&\sigma^2\mathbf{I}_n\left(\tilde{\mathbf{X}}_2^\mathsf{T}\tilde{\mathbf{X}}_2\right)^{-1}\\&=&\sigma^2\left(\tilde{\mathbf{X}}_2^\mathsf{T}\tilde{\mathbf{X}}_2\right)^{-1}\end{eqnarray}\] よって \[\hat{\boldsymbol{\beta}}_2\sim \mathrm{N}\left(\boldsymbol{\beta}_2,\sigma^2\left(\tilde{\mathbf{X}}_2^\mathsf{T}\tilde{\mathbf{X}}_2\right)^{-1}\right)\] となる。
ここでカイ二乗分布の定義を確認すると \[\mathbf{x}=\left(x_1,x_2,\cdots,x_k\right)\quad \mathbf{x}\sim \mathrm{N}(\mu,\sigma^2)\] であるとき \[\displaystyle\sum_{i=1}^k\left(\dfrac{x_i-\mu}{\sigma}\right)^2\sim \chi^2\left(k\right)\] と自由度 \(k\) カイ二乗分布に従うが \[\left(\hat{\boldsymbol{\beta}_2}-\boldsymbol{\beta}_2\right)^\mathsf{T}\mathrm{var}\left(\hat{\boldsymbol{\beta}_2}\right)^{-1}\left(\hat{\boldsymbol{\beta}_2}-\boldsymbol{\beta}_2\right)\] を考えたとき、 \[\left(\hat{\boldsymbol{\beta}_2}-\boldsymbol{\beta}_2\right)^\mathsf{T}\mathrm{var}\left(\hat{\boldsymbol{\beta}_2}\right)^{-1}\left(\hat{\boldsymbol{\beta}_2}-\boldsymbol{\beta}_2\right)=\left(\hat{\boldsymbol{\beta}_2}-\boldsymbol{\beta}_2\right)^\mathsf{T}\dfrac{\tilde{\mathbf{X}_2}^\mathsf{T}\tilde{\mathbf{X}_2}}{\sigma^2}\left(\hat{\boldsymbol{\beta}_2}-\boldsymbol{\beta}_2\right)\] となり、これは \(\boldsymbol{\beta}_2\) の次元 \(k_2\) を自由度とするカイ二乗分布に従う事を表している。 \[\left(\hat{\boldsymbol{\beta}_2}-\boldsymbol{\beta}_2\right)^\mathsf{T}\dfrac{\tilde{\mathbf{X}_2}^\mathsf{T}\tilde{\mathbf{X}_2}}{\sigma^2}\left(\hat{\boldsymbol{\beta}_2}-\boldsymbol{\beta}_2\right)\sim \chi^2{\left(k_2\right)}\tag{3}\] 式(3)をシミュレーションで確認します。
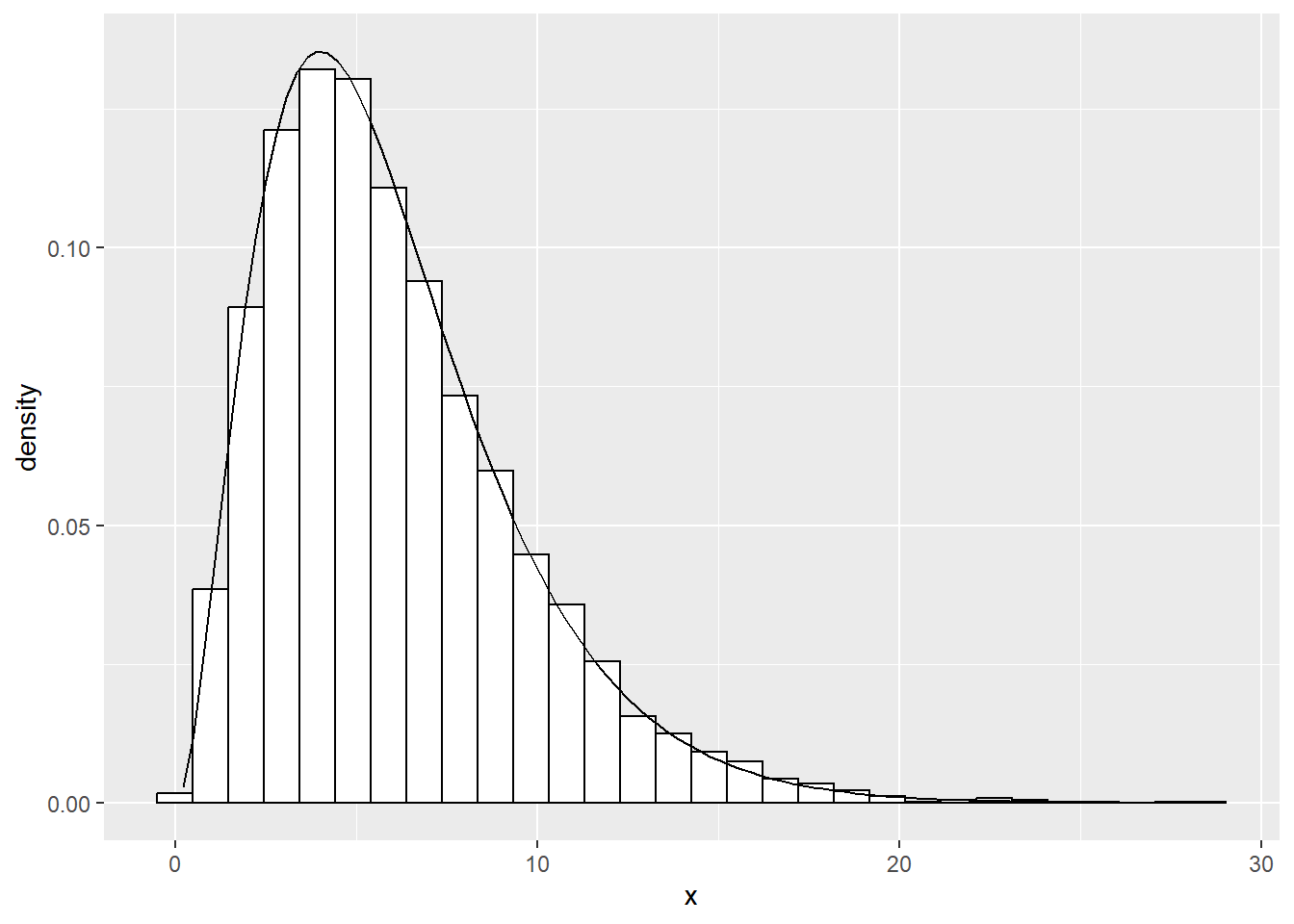
\(k_2=\mathrm{df}=6\) として式(3)をシミュレーションします。
library(dplyr)
seed.base <- 20240715
k <- 10
n <- 200
n.k2 <- 6
iteration <- 10000
test.stat <- vector()
for (iii in seq(iteration)) {
set.seed(seed.base + iii)
X <- rnorm(n = k * n, mean = 0, sd = 1) %>% matrix(nrow = n)
X[, 1] <- 1
beta <- rnorm(n = k) %>% matrix(ncol = 1)
e <- rnorm(n = n, mean = 0, sd = 2)
y <- X %*% beta + e
hat.beta <- solve(t(X) %*% X) %*% t(X) %*% y
hat.beta2 <- hat.beta %>% tail(n.k2)
beta2 <- beta %>% tail(n.k2)
X1 <- X[, k %>% seq() %>% head(-n.k2)]
X2 <- X[, k %>% seq() %>% tail(n.k2)]
tilde.X2 <- X2 - X1 %*% solve(t(X1) %*% X1) %*% t(X1) %*% X2
e <- y - X %*% hat.beta
sigma2 <- sum(e^2) / (n - k)
v <- (t(tilde.X2) %*% tilde.X2) / sigma2
test.stat[iii] <- t(hat.beta2 - beta2) %*% v %*% (hat.beta2 - beta2)
}シミュレーションの結果のヒストグラムと自由度6のカイ二条分布を重ね合わせて確認します。
library(ggplot2)
df <- data.frame(x = test.stat)
ggplot(df, aes(x = x)) +
geom_histogram(aes(y = after_stat(density)),
colour = "black",
fill = "white"
) +
stat_function(fun = dchisq, args = list(df = n.k2), geom = "line")`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.以上です。