こちらの続きです。

なお、式(1)についてはこちらを参照してください。

また、式(3)についてはこちらを参照してください。

以降の数式、導出は https://qiita.com/ykawakubo/items/84759ba5a8d5c5ff3ddd を引用参照しています。
始めに F分布 の定義を確認しますと、自由度がそれぞれ \(d_1\)、\(d_2\) のカイ二乗分布に従う2つの変数を \(U_1\)、\(U_2\) としたとき、\(U_1\)、\(U_2\) が統計学的に独立である場合、両変数の比が従う分布が F分布 となります(参照資料: https://ja.wikipedia.org/wiki/F%E5%88%86%E5%B8%83)。 \[F=\dfrac{U_1/d_1}{U_2/d_2}\] それでは、\(\mathbf{y}\left(n\times 1\right)\)、\(\mathbf{X}\left(n\times k\right)\)、\(\boldsymbol{\beta}\left(k\times1\right)\)、\(\boldsymbol{\epsilon}\left(n\times1\right),\,\boldsymbol{\epsilon}\sim\mathrm{N}\left(0,\sigma^2\mathbf{I}_n\right)\) とした線形モデルを考えます。
ここで \(\mathbf{X}\) を \(\mathbf{X}_1(n\times k_1)\) と \(\mathbf{X}_2(n\times k_2)\) に分割します( \(k=k_1+k_2\) )。 \[\begin{eqnarray}\mathbf{y}&=&\mathbf{X}_1\boldsymbol{\beta}_1+\mathbf{X}_2\boldsymbol{\beta}_2+\boldsymbol{\epsilon}\\\boldsymbol{\beta}&=&\left(\boldsymbol{\beta}_1^{\mathsf{T}},\boldsymbol{\beta}_2^{\mathsf{T}}\right)^{\mathsf{T}}\end{eqnarray}\] よって、OLS推定量 \(\hat{\boldsymbol{\beta}}\) は \[\hat{\boldsymbol{\beta}}=\left(\hat{\boldsymbol{\beta}}_1^{\mathsf{T}},\hat{\boldsymbol{\beta}}_2^{\mathsf{T}}\right)^{\mathsf{T}}\] と表わすことが出来ます。
続いて次の仮説検定を考えます。 \[\mathrm{H}_0: \boldsymbol{\beta}_2=0,\quad\mathrm{H}_1: \boldsymbol{\beta}_2\neq0\] その時、 \[\left(\hat{\boldsymbol{\beta}_2}-\boldsymbol{\beta}_2\right)^\mathsf{T}\dfrac{\tilde{\mathbf{X}_2}^\mathsf{T}\tilde{\mathbf{X}_2}}{\sigma^2}\left(\hat{\boldsymbol{\beta}_2}-\boldsymbol{\beta}_2\right)=\dfrac{\left(\tilde{\mathbf{X}_2}\left(\hat{\boldsymbol{\beta}_2}-\boldsymbol{\beta}_2\right)\right)^\mathsf{T}\left(\tilde{\mathbf{X}_2}\left(\hat{\boldsymbol{\beta}_2}-\boldsymbol{\beta}_2\right)\right)}{\sigma^2}\sim \chi^2{\left(k_2\right)}\tag{1}\] は、\(\boldsymbol{\beta}_2=0\) とすると \[\dfrac{\left(\tilde{\mathbf{X}_2}\left(\hat{\boldsymbol{\beta}_2}-\boldsymbol{\beta}_2\right)\right)^\mathsf{T}\left(\tilde{\mathbf{X}_2}\left(\hat{\boldsymbol{\beta}_2}-\boldsymbol{\beta}_2\right)\right)}{\sigma^2}=\dfrac{\left(\tilde{\mathbf{X}_2}\hat{\boldsymbol{\beta}_2}\right)^\mathsf{T}\left(\tilde{\mathbf{X}_2}\hat{\boldsymbol{\beta}_2}\right)}{\sigma^2}\sim\chi_{k_2}^2\tag{2}\] となります。
続いて、\[\dfrac{\hat{\boldsymbol{\epsilon}}^\mathsf{T}\hat{\boldsymbol{\epsilon}}}{\sigma^2}=\dfrac{(n-k)\hat{\sigma}^2}{\sigma^2}\sim\chi^2_{n-k}\tag{3}\] であるため、式(2)、式(3)から
\(U_1=\dfrac{\left(\tilde{\mathbf{X}_2}\hat{\boldsymbol{\beta}_2}\right)^\mathsf{T}\left(\tilde{\mathbf{X}_2}\hat{\boldsymbol{\beta}_2}\right)}{\sigma^2}\)、\(d_1=k_2\)、\(U_2=\dfrac{(n-k)\hat{\sigma}^2}{\sigma^2}\)、\(d_2=n-k\) としますと、 \[F=\dfrac{U_1/d_1}{U_2/d_2}=\dfrac{\dfrac{\left(\tilde{\mathbf{X}_2}\hat{\boldsymbol{\beta}_2}\right)^\mathsf{T}\left(\tilde{\mathbf{X}_2}\hat{\boldsymbol{\beta}_2}\right)}{\sigma^2}/k2}{\dfrac{(n-k)\hat{\sigma}^2}{\sigma^2}/(n-k)}\sim F_{k2\,,n-k}\] となり、整理しますと \[F=\dfrac{U_1/d_1}{U_2/d_2}=\dfrac{\dfrac{\left(\tilde{\mathbf{X}_2}\hat{\boldsymbol{\beta}_2}\right)^\mathsf{T}\left(\tilde{\mathbf{X}_2}\hat{\boldsymbol{\beta}_2}\right)}{\sigma^2}/k2}{\dfrac{(n-k)\hat{\sigma}^2}{\sigma^2}/(n-k)}=\dfrac{\left(\tilde{\mathbf{X}_2}\hat{\boldsymbol{\beta}_2}\right)^\mathsf{T}\left(\tilde{\mathbf{X}_2}\hat{\boldsymbol{\beta}_2}\right)/k2}{\hat{\sigma}^2}\sim F_{k2\,,n-k}\tag{4}\] と導けます。
シミュレーションで式(4)確認します。
\(\mathbf{y}(200\times1)\)、\(\mathbf{X}(200\times10)\)、\(\boldsymbol{\beta}(10\times1)\)、\(\boldsymbol{\epsilon}(200\times1)\)、とした線形モデルを作成し、\(\mathbf{X}_1(200\times4)\)、\(\mathbf{X}_2(200\times6)\)、\(\boldsymbol{\beta}_1(4\times1)\)、\(\boldsymbol{\beta}_2(6\times1)\) と分割した上で、シミュレーションにより 10000個 の F値 を作成します。
library(dplyr)
seed.base <- 20240724
k <- 10
n <- 200
k2 <- 6
iteration <- 10000
F.value <- vector()
for (iii in seq(iteration)) {
set.seed(seed.base + iii)
X <- rnorm(n = k * n, mean = 0, sd = 1) %>% matrix(nrow = n)
X[, 1] <- 1
beta <- rnorm(n = k, mean = 0, sd = 1) %>% matrix(ncol = 1)
e <- rnorm(n = n, mean = 0, sd = 100) # 意図的に標準偏差を大きくしています。
y <- X %*% beta + e
hat.beta <- solve(t(X) %*% X) %*% t(X) %*% y
hat.beta2 <- hat.beta %>% tail(k2)
X1 <- X[, k %>% seq() %>% head(-k2)]
X2 <- X[, k %>% seq() %>% tail(k2)]
tilde.X2 <- X2 - X1 %*% solve(t(X1) %*% X1) %*% t(X1) %*% X2
hat.e <- y - X %*% hat.beta
hat.sigma2 <- sum(hat.e^2) / (n - k)
F.value[iii] <- t(tilde.X2 %*% hat.beta2) %*% (tilde.X2 %*% hat.beta2) / k2 / hat.sigma2
}
summarytools::descr(F.value)Descriptive Statistics
F.value
N: 10000
F.value
----------------- ----------
Mean 1.03
Std.Dev 0.60
Min 0.03
Q1 0.59
Median 0.92
Q3 1.35
Max 5.04
MAD 0.54
IQR 0.76
CV 0.59
Skewness 1.22
SE.Skewness 0.02
Kurtosis 2.40
N.Valid 10000.00
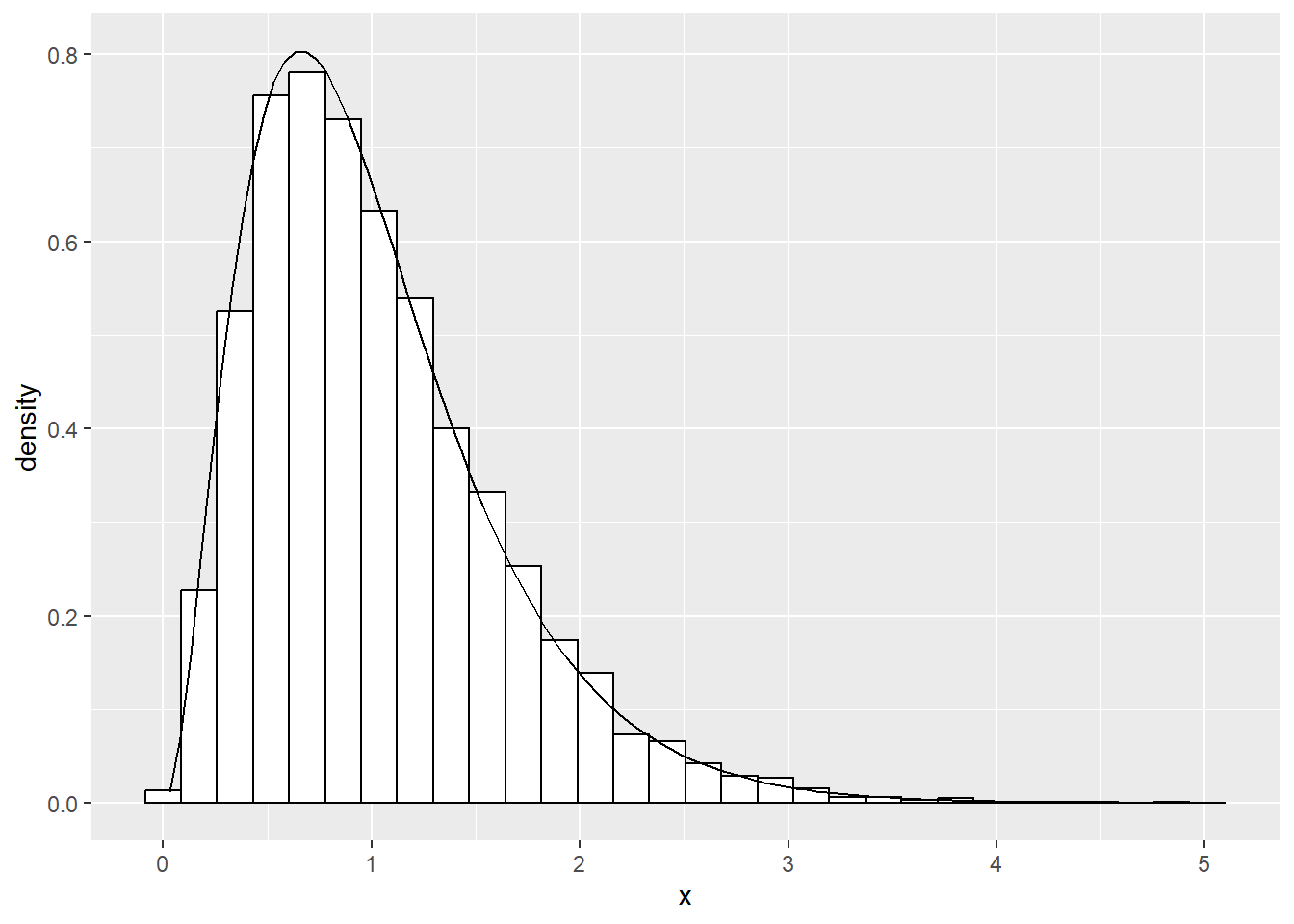
Pct.Valid 100.00F値(F.value) のヒストグラムに \(F_{k2,\,n-k}=F_{6,\,190}\) の確率密度を重ねます。
library(ggplot2)
ggplot(data = data.frame(x = F.value), mapping = aes(x = x)) +
geom_histogram(aes(y = after_stat(density)),
colour = "black",
fill = "white"
) +
stat_function(fun = df, geom = "line", args = list(df1 = k2, df2 = n - k))`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.以上です。