こちらの続きです。

以降の数式、導出は https://qiita.com/ykawakubo/items/84759ba5a8d5c5ff3ddd を引用参照しています。
制約あり とした帰無仮説 \(\mathrm{H}_0:\boldsymbol{\beta}_2=0\) の下での残差は \[\mathbf{y}-\mathbf{X}_1\left(\mathbf{X}_1^\mathsf{T}\mathbf{X}_1\right)^{-1}\mathbf{X}_1^\mathsf{T}\mathbf{y}=\left(\mathbf{I}_n-\mathbf{P}_1\right)\mathbf{y}\tag{1}\] となります。ここで \[\mathbf{P}_1=\mathbf{X}_1\left(\mathbf{X}_1^\mathsf{T}\mathbf{X}_1\right)^{-1}\mathbf{X}_1^\mathsf{T}\] とします。
また 制約なし の場合のモデルは \[\mathbf{y}=\mathbf{X}_1\hat{\boldsymbol{\beta}}_1+\mathbf{X}_2\hat{\boldsymbol{\beta}}_2+\epsilon\] であるため 式(1) は \[\begin{eqnarray}\left(\mathbf{I}_n-\mathbf{P}_1\right)\mathbf{y} &=&\left(\mathbf{I}_n-\mathbf{P}_1\right)\left(\mathbf{X}_1\hat{\boldsymbol{\beta}}_1+\mathbf{X}_2\hat{\boldsymbol{\beta}}_2+\epsilon\right)\\ &=&\left(\mathbf{I}_n-\mathbf{P}_1\right)\mathbf{X}_1\hat{\boldsymbol{\beta}}_1+\left(\mathbf{I}_n-\mathbf{P}_1\right)\mathbf{X}_2\hat{\boldsymbol{\beta}}_2+\left(\mathbf{I}_n-\mathbf{P}_1\right)\boldsymbol{\epsilon} \end{eqnarray}\] と展開できます。
ここで \[\begin{eqnarray} &&\left(\mathbf{I}_n-\mathbf{P}_1\right)\mathbf{X}_1=0\tag{2}\\ &&\left(\mathbf{I}_n-\mathbf{P}_1\right)\mathbf{X}_2=\tilde{\mathbf{X}}_2\tag{3}\\ &&\left(\mathbf{I}_n-\mathbf{P}\right)\mathbf{y}=\boldsymbol{\epsilon}\tag{4}\end{eqnarray}\] である故 \[\begin{eqnarray}\left(\mathbf{I}_n-\mathbf{P}_1\right)\mathbf{y} &=&\left(\mathbf{I}_n-\mathbf{P}_1\right)\left(\mathbf{X}_1\hat{\boldsymbol{\beta}}_1+\mathbf{X}_2\hat{\boldsymbol{\beta}}_2+\epsilon\right)\\ &=&\left(\mathbf{I}_n-\mathbf{P}_1\right)\mathbf{X}_1\hat{\boldsymbol{\beta}}_1+\left(\mathbf{I}_n-\mathbf{P}_1\right)\mathbf{X}_2\hat{\boldsymbol{\beta}}_2+\left(\mathbf{I}_n-\mathbf{P}_1\right)\boldsymbol{\epsilon}\\ &=&\tilde{\mathbf{X}}_2\hat{\boldsymbol{\beta}}_2+\left(\mathbf{I}_n-\mathbf{P}_1\right)\left(\mathbf{I}_n-\mathbf{P}\right)\mathbf{y}\tag{5} \end{eqnarray}\] となります。
なお、式(2)、式(3) についてはこちらを参照してください。

さらに、式(5) の右辺第二項は \[\begin{eqnarray}\left(\mathbf{I}_n-\mathbf{P}_1\right)\left(\mathbf{I}_n-\mathbf{P}\right)=\mathbf{I}_n-\mathbf{P}-\mathbf{P}_1+\mathbf{P}_1\mathbf{P}\end{eqnarray}\] と展開されますが、\(\mathbf{P}_1\)、\(\mathbf{P}\) はいずれも冪等行列であるため、それぞれ列空間 \(\mathbf{X}_1\) と \(\mathbf{X}\) への射影行列であり、さらに \(\mathbf{X}_1 \subset \mathbf{X}\) でもあるため \[\mathbf{P}_1\mathbf{P}=\mathbf{P}\mathbf{P}_1=\mathbf{P}_1\] が成り立ち、よって \[\begin{eqnarray}\left(\mathbf{I}_n-\mathbf{P}_1\right)\left(\mathbf{I}_n-\mathbf{P}\right)&=&\mathbf{I}_n-\mathbf{P}-\mathbf{P}_1+\mathbf{P}_1\mathbf{P}\\&=&\mathbf{I}_n-\mathbf{P}\end{eqnarray}\] となります。 同様に \[\begin{eqnarray}\left(\mathbf{I}_n-\mathbf{P}\right)\left(\mathbf{I}_n-\mathbf{P}_1\right)&=&\mathbf{I}_n-\mathbf{P}_1-\mathbf{P}+\mathbf{P}\mathbf{P}_1\\&=&\mathbf{I}_n-\mathbf{P}\end{eqnarray}\] も成り立ちます。
具体例で確認します。
library(dplyr)
n.row <- 4
n.col <- 3
n <- n.row * n.col
break.point <- 2
X <- rnorm(n) %>% matrix(nrow = n.row)
X1 <- X[, seq(break.point)]
X2 <- X[, (break.point + 1):n.col, drop = F]
P <- X %*% solve(t(X) %*% X) %*% t(X)
P1 <- X1 %*% solve(t(X1) %*% X1) %*% t(X1)
list(P1 = P1, P = P)$P1
[,1] [,2] [,3] [,4]
[1,] 0.4235439 0.1865292 -0.4269299 0.1645969
[2,] 0.1865292 0.4764992 0.1279981 0.4452764
[3,] -0.4269299 0.1279981 0.6835885 0.1328253
[4,] 0.1645969 0.4452764 0.1328253 0.4163684
$P
[,1] [,2] [,3] [,4]
[1,] 0.7672330 0.3288422 -0.1668352 -0.2064349
[2,] 0.3288422 0.5354274 0.2356968 0.2916414
[3,] -0.1668352 0.2356968 0.8804213 -0.1479617
[4,] -0.2064349 0.2916414 -0.1479617 0.8169183\(\mathbf{P}_1\mathbf{P}=\mathbf{P}\mathbf{P}_1=\mathbf{P}_1\) となっていることを確認します。
round(P1 %*% P, 10) == round(P1, 10) [,1] [,2] [,3] [,4]
[1,] TRUE TRUE TRUE TRUE
[2,] TRUE TRUE TRUE TRUE
[3,] TRUE TRUE TRUE TRUE
[4,] TRUE TRUE TRUE TRUEround(P %*% P1, 10) == round(P1, 10) [,1] [,2] [,3] [,4]
[1,] TRUE TRUE TRUE TRUE
[2,] TRUE TRUE TRUE TRUE
[3,] TRUE TRUE TRUE TRUE
[4,] TRUE TRUE TRUE TRUE従って 式(5)、つまり 制約あり( \(\mathrm{H}_0:\boldsymbol{\beta}_2=0\) )のモデルの下での残差は \[\begin{eqnarray}\left(\mathbf{I}_n-\mathbf{P}_1\right)\mathbf{y} &=&\left(\mathbf{I}_n-\mathbf{P}_1\right)\left(\mathbf{X}_1\hat{\boldsymbol{\beta}}_1+\mathbf{X}_2\hat{\boldsymbol{\beta}}_2+\epsilon\right)\\ &=&\left(\mathbf{I}_n-\mathbf{P}_1\right)\mathbf{X}_1\hat{\boldsymbol{\beta}}_1+\left(\mathbf{I}_n-\mathbf{P}_1\right)\mathbf{X}_2\hat{\boldsymbol{\beta}}_2+\left(\mathbf{I}_n-\mathbf{P}_1\right)\boldsymbol{\epsilon}\\ &=&\tilde{\mathbf{X}}_2\hat{\boldsymbol{\beta}}_2+\left(\mathbf{I}_n-\mathbf{P}_1\right)\left(\mathbf{I}_n-\mathbf{P}\right)\mathbf{y}\\ &=&\tilde{\mathbf{X}}_2\hat{\boldsymbol{\beta}}_2+\left(\mathbf{I}_n-\mathbf{P}\right)\mathbf{y} \\&=&\tilde{\mathbf{X}}_2\hat{\boldsymbol{\beta}}_2+\boldsymbol{\epsilon}\end{eqnarray}\] となり、その平方和(残差平方和 Residual Sum of Squares, RSS )は \[\begin{eqnarray}\mathrm{RSS}_\mathrm{R}&=&\left(\tilde{\mathbf{X}}_2\hat{\boldsymbol{\beta}}_2+\boldsymbol{\epsilon}\right)^\mathsf{T}\left(\tilde{\mathbf{X}}_2\hat{\boldsymbol{\beta}}_2+\boldsymbol{\epsilon}\right)\\&=&\hat{\boldsymbol{\beta}}_2^\mathsf{T}\tilde{\mathbf{X}}_2^\mathsf{T}\tilde{\mathbf{X}}_2\hat{\boldsymbol{\beta}}_2+\boldsymbol{\epsilon}^\mathsf{T}\boldsymbol{\epsilon}+2\boldsymbol{\epsilon}^\mathsf{T}\tilde{\mathbf{X}}_2\hat{\boldsymbol{\beta}}_2\tag{6}\end{eqnarray}\] となりますが、式(6) の右辺第三項は \[\begin{eqnarray}\boldsymbol{\epsilon}^\mathsf{T}\tilde{\mathbf{X}}_2&=&\left(\left(\mathbf{I}_n-\mathbf{P}\right)\mathbf{y}\right)^\mathsf{T}\left(\mathbf{I}_n-\mathbf{P}_1\right)\mathbf{X}_2\\ &=&\mathbf{y}^\mathsf{T}\left(\mathbf{I}_n-\mathbf{P}\right)^\mathsf{T}\left(\mathbf{I}_n-\mathbf{P}_1\right)\mathbf{X}_2\\ &=&\mathbf{y}^\mathsf{T}\left(\mathbf{I}_n-\mathbf{P}\right)\left(\mathbf{I}_n-\mathbf{P}_1\right)\mathbf{X}_2\\&=&\mathbf{y}^\mathsf{T}\left(\mathbf{I}_n-\mathbf{P}\right)\left(\mathbf{I}_n-\mathbf{P}_1\right)\mathbf{X}_2\\&=&\mathbf{y}^\mathsf{T}\left(\mathbf{I}_n-\mathbf{P}\right)\mathbf{X}_2\tag{7}\end{eqnarray}\] と展開され、\(\mathbf{X}_2 \subset \mathbf{X}\) であることから \(\mathbf{P}\mathbf{X}_2\) は \[\mathbf{P}\mathbf{X}_2=\mathbf{X}_2\] となり、式(7) は \(\left(\mathbf{I}_n-\mathbf{P}\right)\mathbf{X}_2=\mathbf{X}_2-\mathbf{P}\mathbf{X}_2=0\) であることから \[\boldsymbol{\epsilon}^\mathsf{T}\tilde{\mathbf{X}}_2=0\] となりますので \[\mathrm{RSS}_{\mathrm{R}}=\hat{\boldsymbol{\beta}}_2^\mathsf{T}\tilde{\mathbf{X}}_2^\mathsf{T}\tilde{\mathbf{X}}_2\hat{\boldsymbol{\beta}}_2+\boldsymbol{\epsilon}^\mathsf{T}\boldsymbol{\epsilon}\tag{8}\] となります。
また、式(8) の右辺第二項は 制約なし モデルの残差平方和 \(\mathrm{RSS}_{\mathrm{UR}}\) であるため \[\mathrm{RSS}_{\mathrm{R}}-\mathrm{RSS}_{\mathrm{UR}}=\hat{\boldsymbol{\beta}}_2^\mathsf{T}\tilde{\mathbf{X}}_2^\mathsf{T}\tilde{\mathbf{X}}_2\hat{\boldsymbol{\beta}}_2\] となります。
さらに、\[\hat{\sigma}^2=\dfrac{\hat{\boldsymbol{\epsilon}}^\mathsf{T}\hat{\boldsymbol{\epsilon}}}{n-k}\tag{9}\] であるため \[\hat{\sigma}^2=\dfrac{\mathrm{RSS}_{\mathrm{UR}}}{n-k}\tag{10}\] であり
こちら

の 式(4) の F値 は \[\mathrm{F}=\dfrac{\left(制約ありモデルの残差平方和-制約なしモデルの残差平方和\right)/説明変数の制約の個数}{制約なしモデルの残差平方和/\left(サンプルサイズ-説明変数の個数\right)}\tag{11}\] と表すことが出来ます。
以上の F値 を応用した検定の1つが Chow検定(チョウ検定) です。
以降の数式、導出は https://www.fbc.keio.ac.jp/~tyabu/econometrics/econome1_7.pdf を引用参照しています。
構造変化のモデルを以下の通りとします。
\[\begin{eqnarray} y_t&=&\alpha^{(1)}+\beta_1^{(1)}x_{1,t}+\cdots+\beta_k^{(1)}x_{k,t}+u_t\quad\textrm{for}\, t=1,2,\cdots,T_{B}\\ y_t&=&\alpha^{(2)}+\beta_1^{(2)}x_{1,t}+\cdots+\beta_k^{(2)}x_{k,t}+u_t\quad\textrm{for}\, t=T_{B}+1,\cdots,T \end{eqnarray}\]
また、帰無仮説は \[\begin{eqnarray} \mathrm{H}_0:\alpha^{(1)}=\alpha^{(2)},\beta^{(1)}_1=\beta^{(2)}_1,\cdots,\beta^{(1)}_k=\beta^{(2)}_k \end{eqnarray}\] とし、制約なし モデルは \(\mathrm{H}_0\) が棄却される場合のモデルであるため \[y_t=\alpha^{(1)}+\beta_1^{(1)}x_{1,t}+\cdots+\beta_k^{(1)}x_{k,t}+\theta_0D_t+\theta_1D_tx_{1,t}+\cdots+\theta_kD_tx_{k,t}+u_t\] ここで \[\begin{eqnarray} D_t = \begin{cases} 0 & t=1,2,\cdots,T_B \\ 1 & t=T_B+1,\cdots,T \end{cases} \end{eqnarray}\] \[\theta_0=\alpha^{(2)}-\alpha^{(1)},\theta_1=\beta^{(2)}_1-\beta^{(1)}_1,\cdots,\theta_k=\beta^{(2)}_k-\beta^{(1)}_k\] \[\mathrm{H}_0:\theta_0=\theta_1=\cdots=\theta_k=0\] となります。
よって、式(11) の分母の \(\left(サンプルサイズ-説明変数の個数\right)\) は \(T-2(k+1)\) となり、分子の \(説明変数の制約の個数\) は \(k+1\) となります。
さらに、帰無仮説が棄却されない 制約あり モデルは
\[y_t=\alpha+\beta_1x_{1,t}+\cdots+\beta_kx_{k,t}+u_t\] となり、その残差平方和が \(\mathrm{RSS}_{\mathrm{R}}\) になります。
シミュレーションで確認します。なお、有意水準は共通して 5% とします。
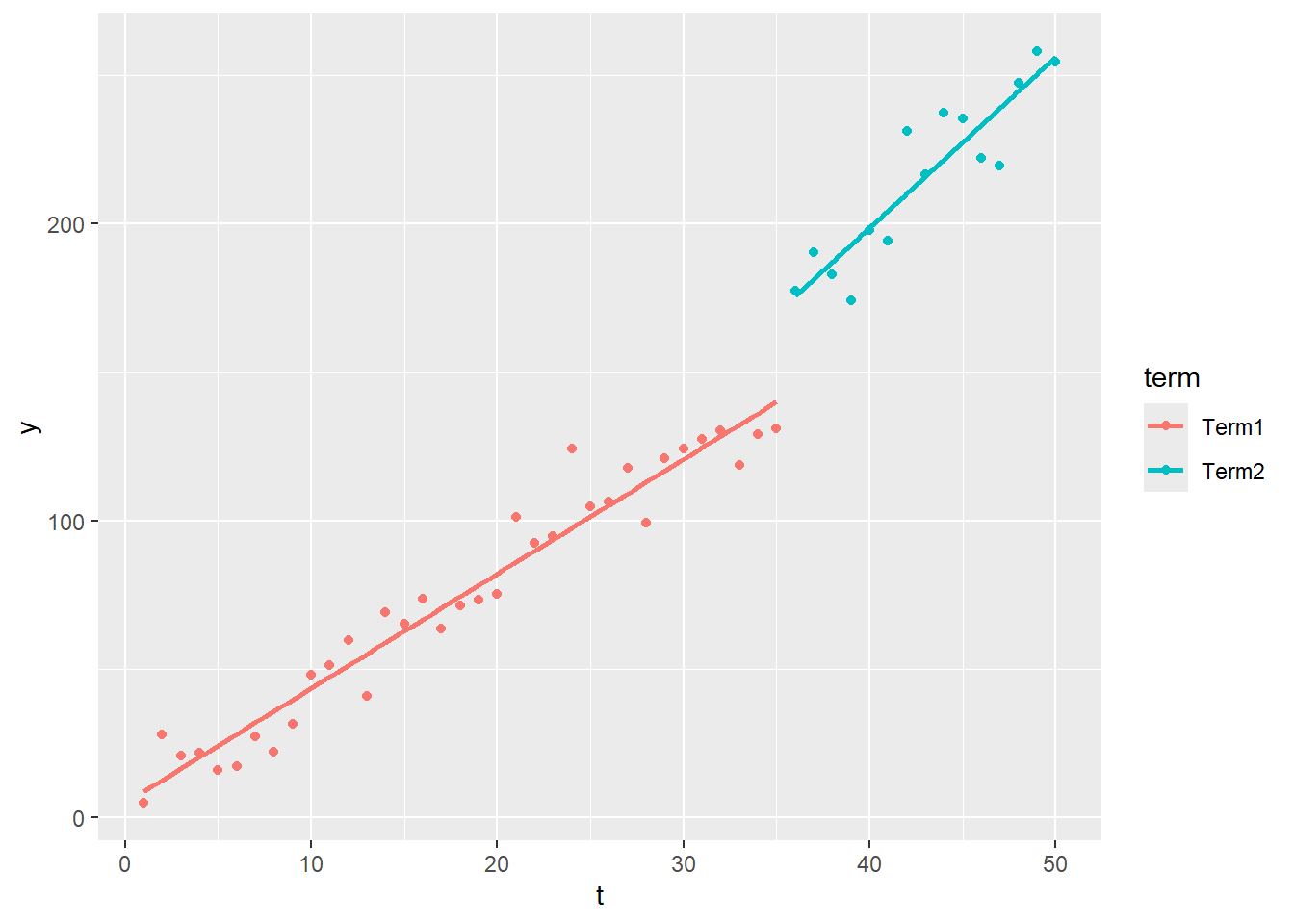
始めに 切片は同一、傾きは異なるモデル の Chow検定(チョウ検定) です。
時点は 50時点 \(t=1,2,\cdots ,50\) とし、構造変化点(break.point)は 35時点目 とします。
傾きは 35時点目 までを \(\beta^{(1)}=4\)、以降を \(\beta^{(2)}=5\) とし、切片は共通して \(\alpha^{(1)}=\alpha^{(2)}=2\) とします。
seed <- 20240730
set.seed(seed = seed)
n <- 50
t <- seq(n)
break.point <- 35
t1 <- seq(break.point)
t2 <- tail(t, -break.point)
a1 <- 2
a2 <- 2
b1 <- 4
b2 <- 5
y1 <- a1 + t1 * b1 + rnorm(length(t1), mean = 0, sd = 10)
y2 <- a2 + t2 * b2 + rnorm(length(t2), mean = 0, sd = 10)
y <- c(y1, y2)
sample.df <- data.frame(t = c(t1, t2), y = c(y1, y2), term = c(rep("Term1", length(t1)), rep("Term2", length(t2))))library(ggplot2)
sample.df %>%
ggplot(mapping = aes(x = t, y = y, col = term)) +
geom_point() +
geom_smooth(method = "lm", se = F)それでは残差平方和を算出します。
始めに 制約あり モデルの残差平方和 \(\mathrm{RSS}_{\mathrm{R}}\) を求めます。
RSS.R <- sum(lm(y ~ t)$resi^2)
RSS.R[1] 12465.05続いて、制約なし モデルの残差平方和 \(\mathrm{RSS}_{\mathrm{UR}}\) を求めます。
RSS.UR <- sum(lm(y1 ~ t1)$resi^2) + sum(lm(y2 ~ t2)$resi^2)
RSS.UR[1] 4798.198F値を算出します。
k <- 2
F.value <- ((RSS.R - RSS.UR) / k) / (RSS.UR / (n - 2 * k))
F.value[1] 36.75078p値を算出します。
pf(q = F.value, df1 = k, df2 = n - 2 * k, lower.tail = F)[1] 2.909629e-1035時点目の前後で切片と傾きがいずれも同一である とする帰無仮説は棄却されます。
なお、Chow検定(チョウ検定) は 関数 sctest {strucchange} を利用できます。
library(strucchange)
sctest(y ~ t, type = "Chow", point = break.point)
Chow test
data: y ~ t
F = 36.751, p-value = 2.91e-10F値、p値とも結果は同じです。
Chow検定(チョウ検定) の関数を作成して、傾きは同一、切片は異なるモデル と 傾き、切片とも同一のモデル を確認します。
以下がF値、p値を求める関数です。
fun_chow_test <- function(n, break.point, a1, a2, b1, b2) {
seed <- 20240730
set.seed(seed = seed)
t <- seq(n)
t1 <- seq(break.point)
t2 <- tail(t, -break.point)
y1 <- a1 + t1 * b1 + rnorm(length(t1), mean = 0, sd = 10)
y2 <- a2 + t2 * b2 + rnorm(length(t2), mean = 0, sd = 10)
y <- c(y1, y2)
RSS.R <- sum(lm(y ~ t)$resi^2)
RSS.UR <- sum(lm(y1 ~ t1)$resi^2) + sum(lm(y2 ~ t2)$resi^2)
F.value <- ((RSS.R - RSS.UR) / k) / (RSS.UR / (n - 2 * k))
p.value <- pf(q = F.value, df1 = k, df2 = n - 2 * k, lower.tail = F)
return(list(y = y, t = t, F.value = F.value, p.value = p.value))
}始めに 傾きは同一、切片は異なるモデル を検定します。
傾きは \(\beta^{(1)}=\beta^{(2)}=4\) と同一、切片は \(\alpha^{(1)}=5,\,\alpha^{(2)}=20\) とし、構造変化点は 20時点目 として検定します。
break.point <- 20
result <- fun_chow_test(n = n, break.point = break.point, a1 = 5, a2 = 20, b1 = 4, b2 = 4)
result$y
[1] 7.712608 31.011738 23.684127 24.542395 18.759098 20.289923
[7] 30.225628 24.946752 34.458660 51.034330 54.202636 62.703578
[13] 43.905064 72.175582 68.232873 76.576612 66.669035 74.338422
[19] 76.332813 78.251071 119.255753 110.535973 112.567438 142.064553
[25] 122.806234 124.504290 135.827428 117.132343 138.836167 142.302141
[31] 145.618454 148.329840 136.748337 147.059047 149.155764 159.312711
[37] 171.561888 162.939902 153.280326 175.738765 171.251284 207.237087
[43] 191.549667 211.606866 208.649757 194.152305 190.668266 217.588735
[49] 227.155250 222.582279
$t
[1] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
[26] 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
$F.value
[1] 6.400122
$p.value
[1] 0.00352947520時点目の前後で切片、傾きいずれも同一 とする帰無仮説は棄却されます。
sctest(result$y ~ result$t, type = "Chow", point = break.point)
Chow test
data: result$y ~ result$t
F = 6.4001, p-value = 0.003529関数 sctest {strucchange} の結果と一致します。
最後に 傾き、切片とも同一のモデル を検定します。
傾きは \(\beta^{(1)}=\beta^{(2)}=4\) と同一とし、切片も \(\alpha^{(1)}=\alpha^{(2)}=20\) と同一、構造変化点は 40時点目 として検定します。
break.point <- 40
result <- fun_chow_test(n = n, break.point = break.point, a1 = 20, a2 = 20, b1 = 4, b2 = 4)
result$y
[1] 22.71261 46.01174 38.68413 39.54240 33.75910 35.28992 45.22563
[8] 39.94675 49.45866 66.03433 69.20264 77.70358 58.90506 87.17558
[15] 83.23287 91.57661 81.66903 89.33842 91.33281 93.25107 119.25575
[22] 110.53597 112.56744 142.06455 122.80623 124.50429 135.82743 117.13234
[29] 138.83617 142.30214 145.61845 148.32984 136.74834 147.05905 149.15576
[36] 159.31271 171.56189 162.93990 153.28033 175.73877 171.25128 207.23709
[43] 191.54967 211.60687 208.64976 194.15231 190.66827 217.58874 227.15525
[50] 222.58228
$t
[1] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
[26] 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
$F.value
[1] 1.446863
$p.value
[1] 0.2458148切片、傾きいずれも同一 とする帰無仮説は棄却されません。
sctest(result$y ~ result$t, type = "Chow", point = break.point)
Chow test
data: result$y ~ result$t
F = 1.4469, p-value = 0.2458こちらも関数 sctest {strucchange} の結果と一致します。
以上です。