交差エントロピーとカルバック･ライブラー情報量

こちらの続きです。

連続確率分布の平均情報量(エントロピー)
...
www.saecanet.com
2024.08.25

交差エントロピー(クロスエントロピー) 及び カルバック･ライブラー情報量(Kullback-Leibler情報量、カルバック･ライブラー･ダイバージェンス) の定義を確認します。

以降の数式、導出は以下の資料を参照引用しています。

  1. http://www.mi.u-tokyo.ac.jp/mds-oudan/lecture_document_2019_math7/%E6%99%82%E7%B3%BB%E5%88%97%E8%A7%A3%E6%9E%90%EF%BC%88%EF%BC%93%EF%BC%89_2019.pdf
  2. https://ja.wikipedia.org/wiki/%E4%BA%A4%E5%B7%AE%E3%82%A8%E3%83%B3%E3%83%88%E3%83%AD%E3%83%94%E3%83%BC

始めに 交差エントロピー の定義を確認します。

真の分布を \(p(x)\)、モデルの分布を \(g(x)\) としたとき(以下同様)、\(p\)、\(q\) がいずれも 離散確率分布 の場合は

\[H(p,q)=-\displaystyle\sum p(x)\log q(x)\] 連続確率分布 の場合は

\[H(p,q)=-\displaystyle\int_{-\infty}^\infty p(x)\log q(x)\,dx\]

続いて カルバック･ライブラー情報量 の定義を確認します。

離散確率分布 の場合は

\[D_{\mathrm{KL}}(p\parallel q)=\displaystyle\sum p(x)\log\dfrac{p(x)}{q(x)}\]

連続確率分布 の場合は

\[D_{\mathrm{KL}}(p\parallel q)=\displaystyle\int_{-\infty}^\infty p(x)\log\dfrac{p(x)}{q(x)}\,dx\] それでは、2つの 一変量正規分布 を具体例として カルバック･ライブラー情報量 を確認します。

一変量正規分布間 の カルバック･ライブラー情報量 は以下の通りです。

\[ D_{\mathrm{KL}}(p\parallel q) = \log \dfrac{\sigma_2}{\sigma_1} + \dfrac{\sigma_1^2 + (\mu_1 - \mu_2)^2}{2\sigma^2_2} - \dfrac{1}{2} \]

参考引用資料

  1. https://statproofbook.github.io/P/norm-kl.html
  2. https://en.wikipedia.org/wiki/Kullback%E2%80%93Leibler_divergence
  3. https://sucrose.hatenablog.com/entry/2013/07/20/190146

始めにサンプルデータを作成します。

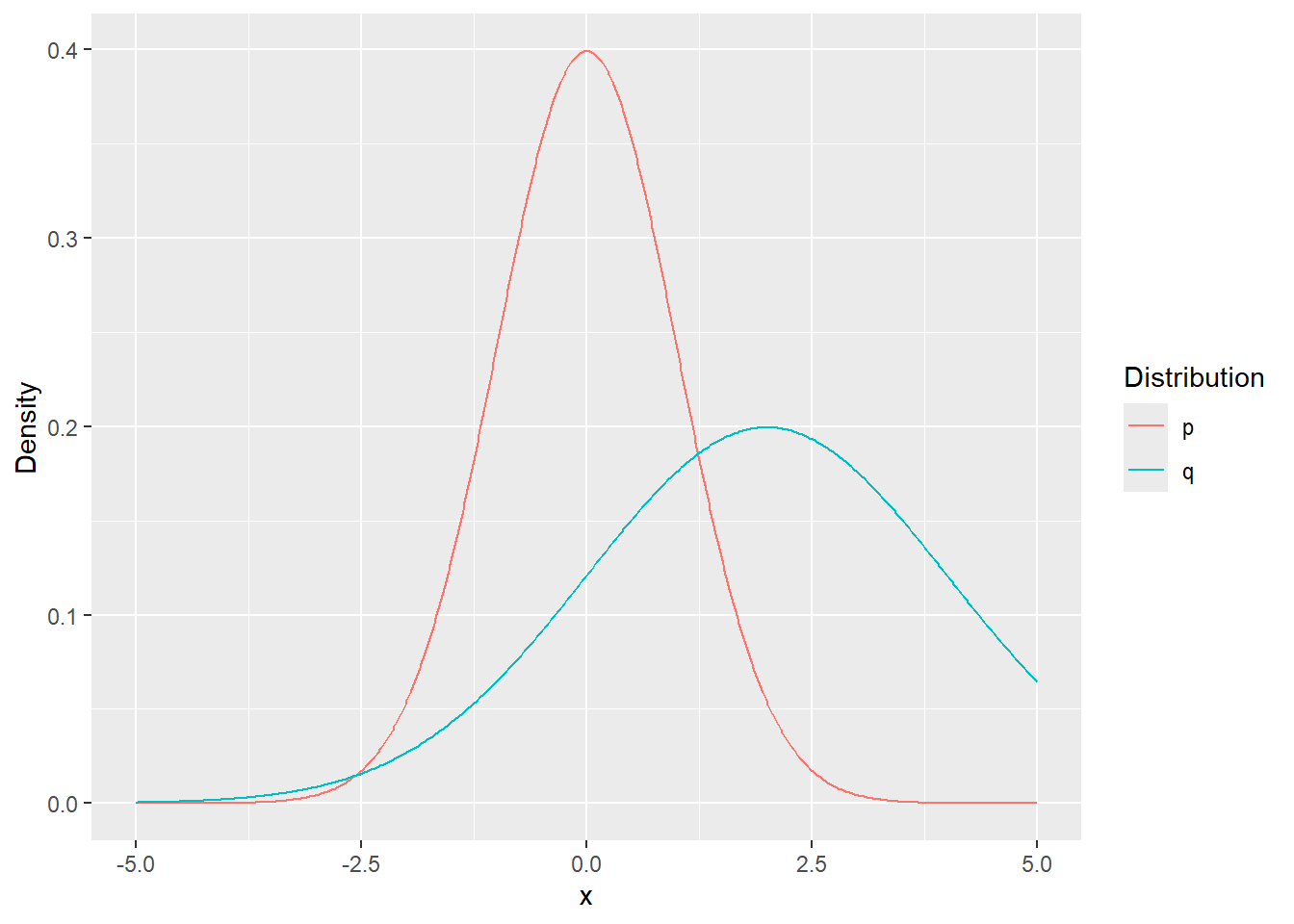
\(p(x)\) は 平均値 が \(\mu_1=0\)、分散が \(\sigma_1^2=1\) の正規分布、\(g(x)\) は 平均値 が \(\mu_2=2\) 、分散が \(\sigma_2^2=4\) の正規分布とします。

library(ggplot2)
library(dplyr)
mu_1 <- 0
mu_2 <- 2
sigma2_1 <- 1
sigma2_2 <- 4
n <- 500
x <- seq(-5, 5, length.out = n)
p <- dnorm(x = x, mean = mu_1, sd = sigma2_1^0.5)
q <- dnorm(x = x, mean = mu_2, sd = sigma2_2^0.5)
tidydf <- data.frame(x, p) %>%
  data.frame(q) %>%
  tidyr::gather(key = "Distribution", value = "Density", colnames(.)[-1])
tidydf %>% ggplot(mapping = aes(x = x, y = Density, colour = Distribution)) +
  geom_line()
Figure 1

カルバック･ライブラー情報量 を求めます。

kl_divergence <- function(mu_1, mu_2, sigma2_1, sigma2_2) {
  log(sigma2_2^0.5 / sigma2_1^0.5) + (sigma2_1 + (mu_1 - mu_2)^2) / (2 * sigma2_2) - 1 / 2
}
kl_divergence(mu_1 = mu_1, mu_2 = mu_2, sigma2_1 = sigma2_1, sigma2_2 = sigma2_2)
[1] 0.8181472

続いて、平均値 および 分散 をそれぞれ変化させた場合の カルバック･ライブラー情報量 の変化を確認します。

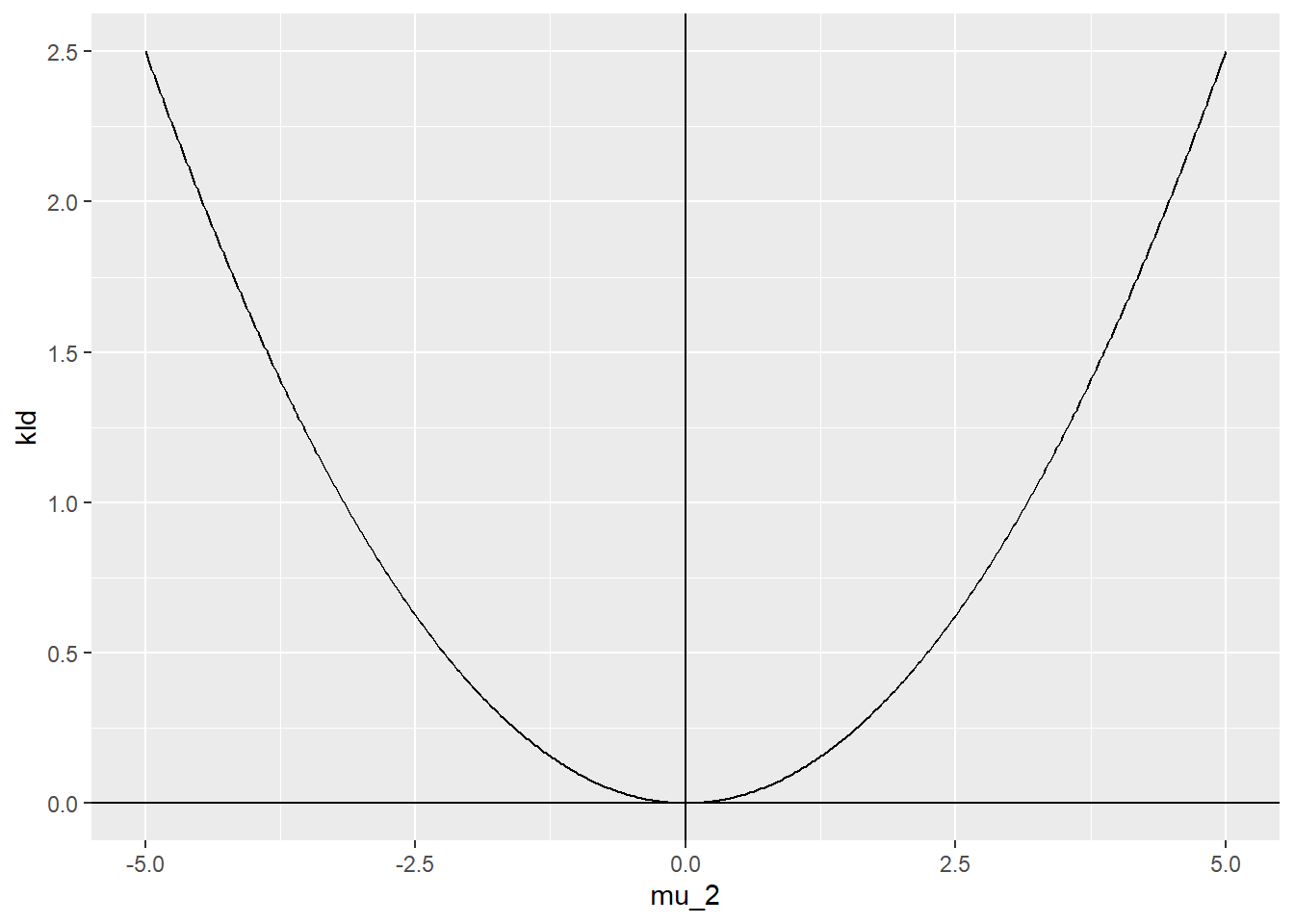
始めに 分散 は同一( \(\sigma_1^2=\sigma_2^2=5\) )とし、平均値 は \(\mu_1=0\)、\(\mu_2\) は -5から5 まで変化させた場合です。

sigma2_1 <- sigma2_2 <- 5
kld <- NULL
mu_2 <- seq(-5, 5, length.out = n)
for (iii in mu_2) {
  kld <- c(kld, kl_divergence(mu_1 = mu_1, mu_2 = iii, sigma2_1 = sigma2_1, sigma2_2 = sigma2_2))
}
ggplot(mapping = aes(x = mu_2, y = kld)) +
  geom_line() +
  geom_hline(yintercept = 0) +
  geom_vline(xintercept = 0)
Figure 2

平均値 が同一(\(\mu_1=\mu_2=0\)) の場合、つまり 同一分布 の場合に カルバック･ライブラー情報量 は 最小(=0) となります。

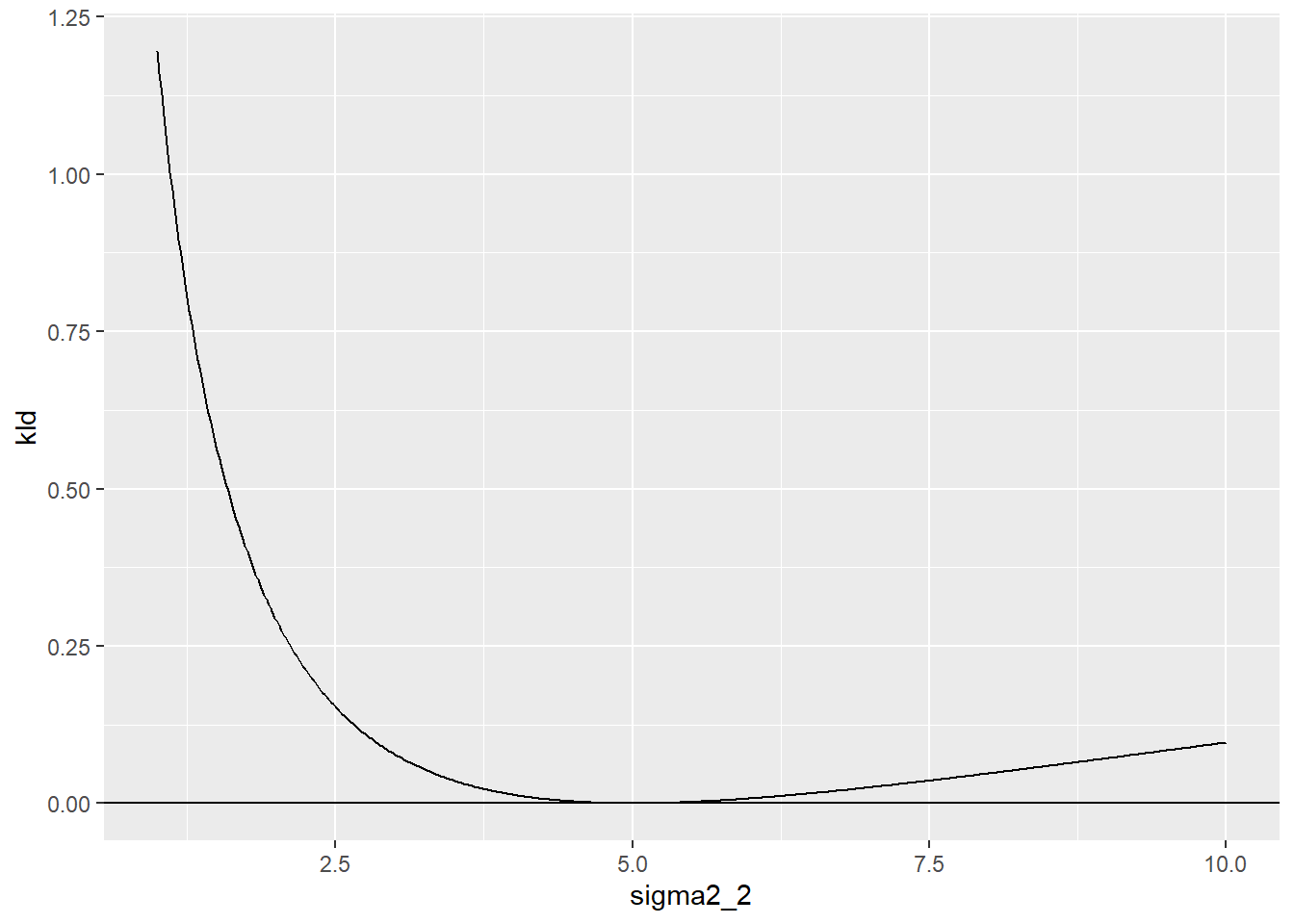
続いて 平均値 は同一(\(\mu_1=\mu_2=0\))とし、分散 は \(\sigma_1^2=5\)、\(\sigma_2^2\) は 1から10 まで変化させた場合です。

mu_2 <- 0
kld <- NULL
sigma2_2 <- seq(1, 10, length.out = n)
for (iii in sigma2_2) {
  kld <- c(kld, kl_divergence(mu_1 = mu_1, mu_2 = mu_2, sigma2_1 = sigma2_1, sigma2_2 = iii))
}
ggplot(mapping = aes(x = sigma2_2, y = kld)) +
  geom_line() +
  geom_hline(yintercept = 0)
Figure 3

分散 が同一(\(\sigma^2_1=\sigma^2_2=5\)) の場合、つまり 同一分布の場合 に カルバック･ライブラー情報量 は 最小(=0) となります。

以上です。