Rでバイリニア型1自由度系システムの地震応答を計算します。
本ポストのデータ(地震波、パラメータ)、数式、導出は全て以下の資料(以降「引用資料」) を引用参照しています。
- https://www.ritsumei.ac.jp/se/rv/izuno/software.html
- 酒井 久和, 澤田 純男, 土岐 憲三, 収束計算を行わない動的非線形FEMのための時間積分法, 土木学会論文集, 1995, 1995 巻, 507 号, p. 137-147
「引用資料1」で公開されています「1自由度系バイリニア型非線形地震応答計算」のエクセルシート(bilinear-j.xlsx)をRで実現します。
始めに以下のパラメータを入力します。
library(dplyr)
Delta_t <- 0.01 # 時間刻み(s)
N <- 3000 # データ数
m <- 740 # 質量(t)
h <- 0.02 # 減衰定数
Py <- 2795 # 降伏耐力(kN)
delta_y <- 0.0265 # 降伏変位(m)
Pu <- 4341 # 終局耐力(kN)
delta_u <- 0.0823 # 終局変位(m)以下は上記入力パラメータのみで決定されるパラメータです。
# 初期剛性(kN/m) = 降伏耐力(kN) / 降伏変位(m)
k1 <- Py / delta_y
# 第2剛性(kN/m) = (終局耐力(kN) - 降伏耐力(kN)) / (終局変位(m) - 降伏変位(m))
k2 <- (Pu - Py) / (delta_u - delta_y)
# 固有円振動数(rad/s) = (初期剛性(kN/m)/質量(t))^0.5
omega <- (k1 / m)^0.5
# 固有振動数(Hz)
f <- omega / 2 / pi
# 固有周期 T(s)
T <- 2 * pi / omega
# 粘性減衰係数(kN・s/m) = 2*減衰定数*(質量*初期剛性)^0.5
viscous_damping_coefficient <- 2 * h * (m * k1)^0.5
list(k1 = k1, k2 = k2, omega = omega, f = f, T = T, viscous_damping_coefficient = viscous_damping_coefficient)$k1
[1] 105471.7
$k2
[1] 27706.09
$omega
[1] 11.93856
$f
[1] 1.900082
$T
[1] 0.5262932
$viscous_damping_coefficient
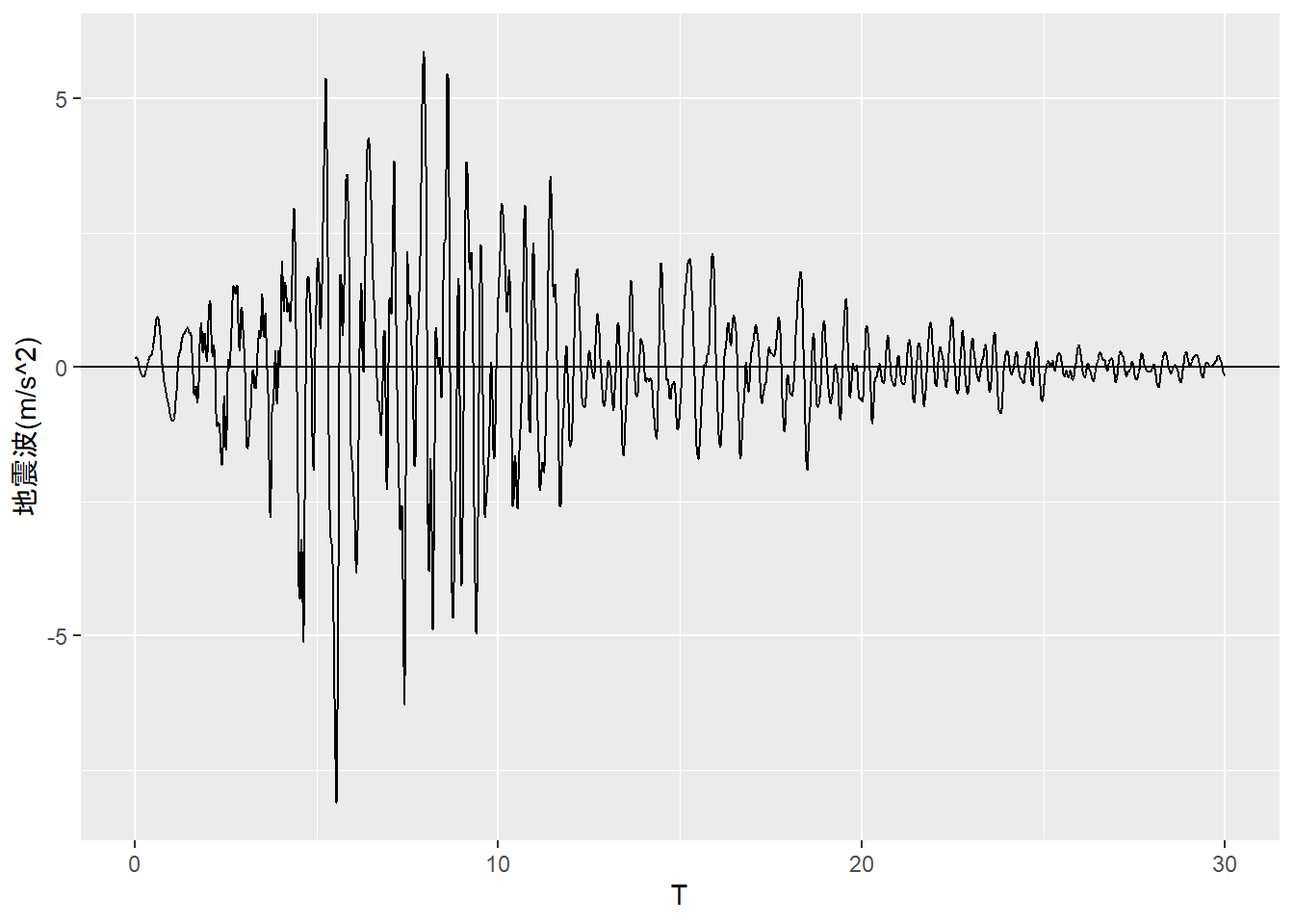
[1] 353.3815サンプルとする地震波(m/s2)は以下のとおりです( Figure 1 )。
library(ggplot2)
T <- Delta_t * seq(N)
ggplot(mapping = aes(x = T, y = earthquake_wave)) +
geom_line() +
geom_hline(yintercept = 0) +
labs(y = "地震波(m/s^2)")最大地震加速度(m/s2)を求めます、
(maximum_earthquake_acceleration <- max(abs(earthquake_wave)))[1] 8.1202以下に各種応答の算出式を記します。
相対変位(m)
\[質量\times\left(4\times\dfrac{相対変位_{t-1}}{\Delta t^2} +4\times \dfrac{相対速度_{t-1}}{\Delta t}+相対加速度_{t-1}\right)\tag{1}\] \[粘性減衰係数\times\left(2\times \dfrac{相対変位_{t-1}}{\Delta t} +相対速度_{t-1}\right)\tag{2}\] \[初期剛性+2\times \dfrac{粘性減衰係数}{\Delta t}+4\times\dfrac{質量}{\Delta t^2}\tag{3}\] \[相対変位_t=\left(-質量\times地震波_t+調整外力_{t-1}+(1)+(2)\right)(3)^{-1}\tag{4}\]
復元力(kN)
「バイリニアの計算には、前ステップからの初期剛性によって決まる点と、正の降伏域にある点、および負の降伏域にある点の3点の復元力を比較し、大きくも小さくもない点を採用するという単純な方法をとっている」
出典 : https://www.ritsumei.ac.jp/se/rv/izuno/software.html
調整外力(kN)
\[調整外力_t=初期剛性\times相対変位_t-復元力_t\tag{5}\]
相対速度(m/s)
\[質量+\Delta t\times \dfrac{粘性減衰係数}{2}\tag{6}\] \[相対速度_t=-\,相対速度_{t-1}+\dfrac{2\times(相対変位_t-相対変位_{t-1})}{\Delta t}+\dfrac{調整外力の増分_t\times\Delta t}{2}\times (6)^{-1}\tag{7}\]
相対加速度(m/s2)
\[相対加速度_t=-相対加速度_{t-1}-4\times\dfrac{相対速度_{t-1}}{\Delta t}+\dfrac{4\times(相対変位_t-相対変位_{t-1})}{\Delta t^2}+調整外力の増分_t\times(6)^{-1}\tag{8}\]
絶対加速度(m/s2)
\[絶対加速度_t=地震波_t+相対加速度_t\tag{9}\]
履歴エネルギー(kN・m)
\[履歴エネルギー_t=\dfrac{(復元力_{t}+復元力_{t-1})\times(相対変位_t-相対変位_{t-1})}{2}\tag{10}\]
入力エネルギー(kN・m)
\[入力エネルギー_t=-\,\dfrac{(地震波_{t-1}\times相対速度_{t-1}+地震波_t\times相対速度_t)\times\Delta t\times質量}{2}\tag{11}\]
累積履歴エネルギー吸収量(kN・m)
\[累積履歴エネルギー吸収量_t=履歴エネルギー_t+累積履歴エネルギー吸収量_{t-1}\tag{12}\]
累積入力エネルギー量(kN・m)
\[累積入力エネルギー量_t=入力エネルギー_t+累積入力エネルギー量_{t-1}\tag{13}\]
最大塑性率
\[最大塑性率=最大応答変位\,\,/\,\,降伏変位\tag{14}\]
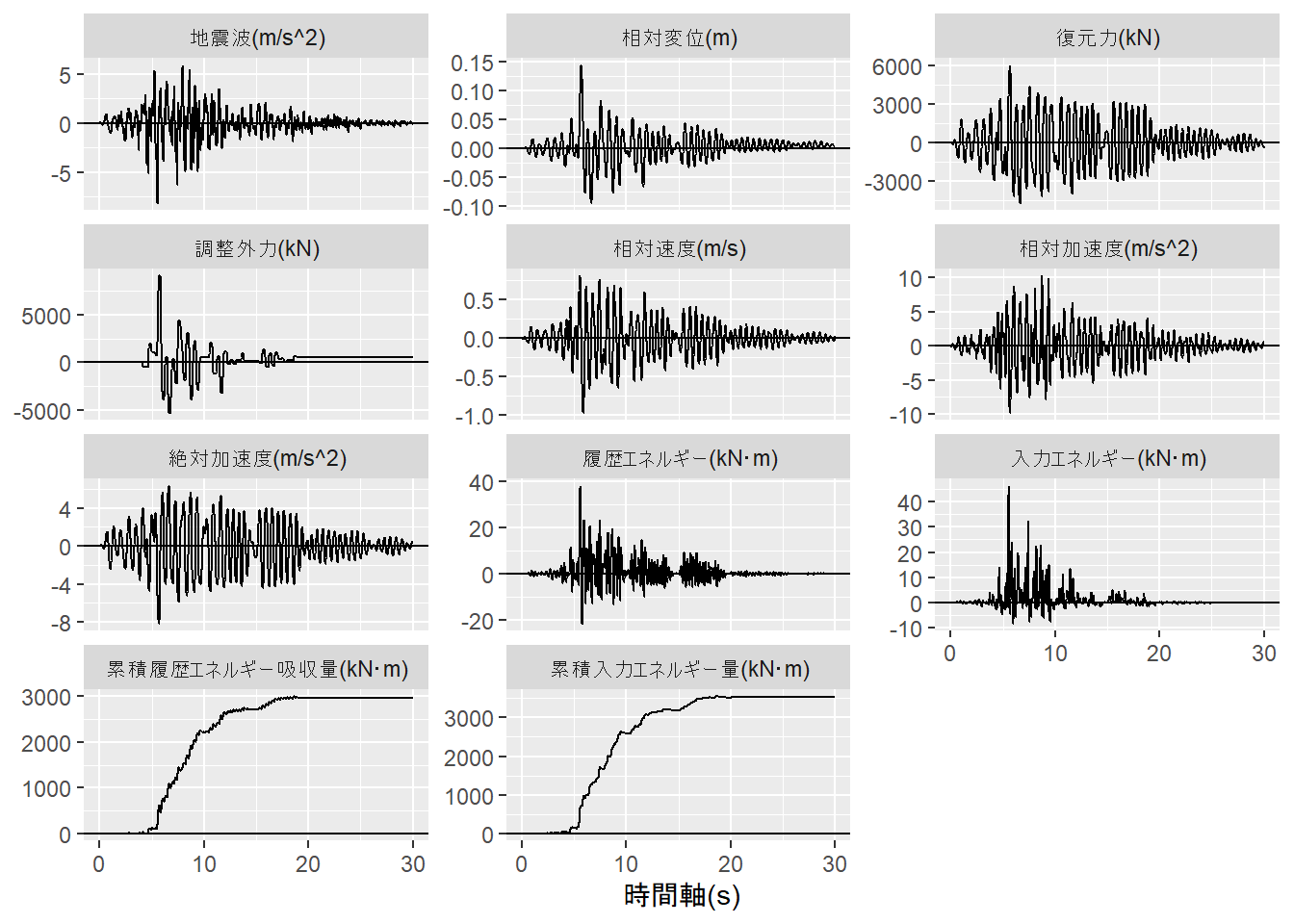
それではサンプル地震波に対する時間刻み毎の応答を求めます。Figure 2 が各種応答の推移です。
relative_displacement <- relative_velocity <- relative_acceleration <- external_force <- hysteretic_energy <- input_energy <- cumulative_hysteretic_energy_absorption <- cumulative_input_energy <- linear_region <- yield_positive <- yield_negative <- restoring <- external_force_diff <- absolute_acceleration <- rep(0, N)
# 式(3)
eq03 <- k1 + 2 * viscous_damping_coefficient / Delta_t + 4 * m / Delta_t^2
# 式(6)
eq06 <- m + Delta_t * viscous_damping_coefficient / 2
for (n in 2:N) {
# 相対変位 式(4)
term1 <- -m * earthquake_wave[n]
term2 <- external_force[n - 1]
eq01_1 <- 4 * relative_displacement[n - 1] / Delta_t^2
eq01_2 <- 4 * relative_velocity[n - 1] / Delta_t
eq01_3 <- relative_acceleration[n - 1]
eq01 <- m * (eq01_1 + eq01_2 + eq01_3)
eq02 <- viscous_damping_coefficient * (2 * relative_displacement[n - 1] / Delta_t + relative_velocity[n - 1])
relative_displacement[n] <- (term1 + term2 + eq01 + eq02) / eq03
# 復元力
linear_region[n] <- k1 * (relative_displacement[n] - relative_displacement[n - 1]) + restoring[n - 1]
yield_positive[n] <- k2 * (relative_displacement[n] - delta_y) + Py
yield_negative[n] <- k2 * (relative_displacement[n] + delta_y) - Py
restoring[n] <- c(linear_region[n], yield_positive[n], yield_negative[n]) %>%
sort() %>%
{
.[2]
}
# 調整外力 式(5)
external_force[n] <- k1 * relative_displacement[n] - restoring[n]
# 調整外力の増分
external_force_diff[n] <- external_force[n] - external_force[n - 1]
# 相対速度 式(7)
relative_velocity[n] <- -1 * relative_velocity[n - 1] + 2 / Delta_t * (relative_displacement[n] - relative_displacement[n - 1]) + external_force_diff[n] * Delta_t / 2 / eq06
# 相対加速度 式(8)
relative_acceleration[n] <- -1 * relative_acceleration[n - 1] - 4 * relative_velocity[n - 1] / Delta_t + 4 / Delta_t^2 * (relative_displacement[n] - relative_displacement[n - 1]) + external_force_diff[n] / eq06
# 履歴エネルギー
hysteretic_energy[n] <- (restoring[n] + restoring[n - 1]) * (relative_displacement[n] - relative_displacement[n - 1]) / 2
# 入力エネルギー
input_energy[n] <- -1 * (earthquake_wave[n - 1] * relative_velocity[n - 1] + earthquake_wave[n] * relative_velocity[n]) * Delta_t / 2 * m
# 累積履歴エネルギー吸収量
cumulative_hysteretic_energy_absorption[n] <- hysteretic_energy[n] + cumulative_hysteretic_energy_absorption[n - 1]
# 累積入力エネルギー量
cumulative_input_energy[n] <- input_energy[n] + cumulative_input_energy[n - 1]
}
# 絶対加速度 式(9)
absolute_acceleration <- earthquake_wave + relative_accelerationdfresponse <-
data.frame(
T,
earthquake_wave,
relative_displacement,
restoring,
external_force,
relative_velocity,
relative_acceleration,
absolute_acceleration,
hysteretic_energy,
input_energy,
cumulative_hysteretic_energy_absorption,
cumulative_input_energy
)
colnames(dfresponse) <-
c(
"時間軸(s)",
"地震波(m/s^2)",
"相対変位(m)",
"復元力(kN)",
"調整外力(kN)",
"相対速度(m/s)",
"相対加速度(m/s^2)",
"絶対加速度(m/s^2)",
"履歴エネルギー(kN・m)",
"入力エネルギー(kN・m)",
"累積履歴エネルギー吸収量(kN・m)",
"累積入力エネルギー量(kN・m)"
)
tidyresponse <- dfresponse %>% tidyr::gather(key = "key", value = "value", colnames(.)[-1])
tidyresponse$key <- tidyresponse$key %>% factor(levels = unique(.))
tidyresponse %>% ggplot(mapping = aes(x = `時間軸(s)`, y = value)) +
geom_line() +
facet_wrap(. ~ key, scale = "free_y", ncol = 3) +
theme(axis.title.y = element_blank()) +
geom_hline(yintercept = 0)最後に各応答の最大値を確認します。
list(
`最大応答加速度(m/s^2)` = max(abs(absolute_acceleration)),
`最大応答変位(m)` = max(abs(relative_displacement)),
`最大応答速度(m/s)` = max(abs(relative_velocity)),
`最大復元力(kN)` = max(abs(restoring)),
`最大塑性率(-)` = max(abs(relative_displacement)) / delta_y
)$`最大応答加速度(m/s^2)`
[1] 8.192681
$`最大応答変位(m)`
[1] 0.1435695
$`最大応答速度(m/s)`
[1] 0.9762597
$`最大復元力(kN)`
[1] 6038.537
$`最大塑性率(-)`
[1] 5.417715以上です。