Rで1自由度系剛性劣化型非線形地震応答を計算します。
本ポストのデータ(地震波、パラメータ)、数式、導出は全て以下の資料(以降「引用資料」) を引用参照しています。
- https://www.ritsumei.ac.jp/se/rv/izuno/software.html
- 酒井 久和, 澤田 純男, 土岐 憲三, 収束計算を行わない動的非線形FEMのための時間積分法, 土木学会論文集, 1995, 1995 巻, 507 号, p. 137-147
「引用資料1」で公開されています「1自由度系剛性劣化型非線形地震応答計算」のエクセルシート(clough-j.xlsx)をRで実現します。
始めに以下のパラメータを入力します。
library(dplyr)
Delta_t <- 0.01 # 時間刻み(s)
N <- 3000 # データ数
m <- 740 # 質量(t)
h <- 0.02 # 減衰定数
Py <- 2795 # 降伏耐力(kN)
delta_y <- 0.0265 # 降伏変位(m)
Pu <- 4341 # 最大耐力(kN)
delta_u <- 0.0823 # 最大耐力時変位(m)以下は上記入力パラメータのみで決定されるパラメータです。
# 初期剛性(kN/m) = 降伏耐力(kN) / 降伏変位(m)
k1 <- Py / delta_y
# 第2剛性(kN/m) = (終局耐力(kN) - 降伏耐力(kN)) / (終局変位(m) - 降伏変位(m))
k2 <- (Pu - Py) / (delta_u - delta_y)
# 固有円振動数(rad/s) = (初期剛性(kN/m)/質量(t))^0.5
omega <- (k1 / m)^0.5
# 固有振動数(Hz)
f <- omega / 2 / pi
# 固有周期 T(s)
T <- 2 * pi / omega
# 粘性減衰係数(kN・s/m) = 2*減衰定数*(質量*初期剛性)^0.5
viscous_damping_coefficient <- 2 * h * (m * k1)^0.5
list(k1 = k1, k2 = k2, omega = omega, f = f, T = T, viscous_damping_coefficient = viscous_damping_coefficient)$k1
[1] 105471.7
$k2
[1] 27706.09
$omega
[1] 11.93856
$f
[1] 1.900082
$T
[1] 0.5262932
$viscous_damping_coefficient
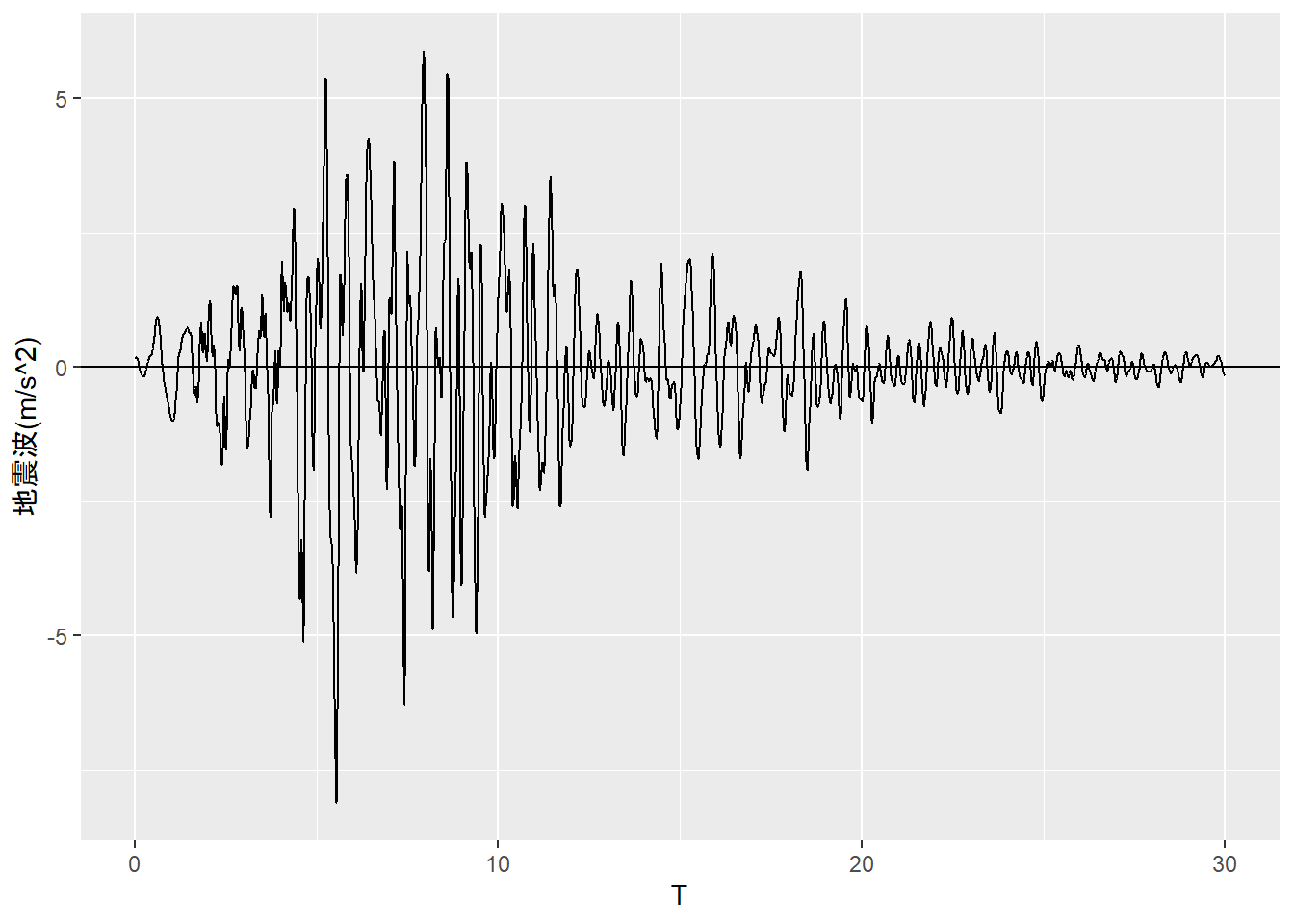
[1] 353.3815サンプルとする地震波(m/s2)は以下のとおりです( Figure 1 )。
library(ggplot2)
T <- Delta_t * seq(N)
ggplot(mapping = aes(x = T, y = earthquake_wave)) +
geom_line() +
geom_hline(yintercept = 0) +
labs(y = "地震波(m/s^2)")最大地震加速度(m/s2)を求めます、
(maximum_earthquake_acceleration <- max(abs(earthquake_wave)))[1] 8.1202以下に各種応答の算出式を記します。
相対変位(m)
\[質量\times\left(4\times\dfrac{相対変位_{t-1}}{\Delta t^2} +4\times \dfrac{相対速度_{t-1}}{\Delta t}+相対加速度_{t-1}\right)\tag{1}\] \[粘性減衰係数\times\left(2\times \dfrac{相対変位_{t-1}}{\Delta t} +相対速度_{t-1}\right)\tag{2}\] \[初期剛性+2\times \dfrac{粘性減衰係数}{\Delta t}+4\times\dfrac{質量}{\Delta t^2}\tag{3}\] \[相対変位_t=\left(-質量\times地震波_t+調整外力_{t-1}+(1)+(2)\right)(3)^{-1}\tag{4}\] 最小変位(m)
\[最小変位_{t=1}=-\,降伏変位\tag{5}\]
\[最小変位_{1<t}=\mathrm{min}\left(相対変位_t\,,\,最小変位_{t-1}\right)\tag{6}\]
最小復元力(kN)
\[最小復元力_{t=1}=-\,降伏耐力\tag{7}\]
\[最小復元力_{1<t}=\mathrm{min}\left( 復元力_{t-1} \,,\, 最小復元力_{t-1}\right)\tag{8}\]
最大変位(m)
\[最大変位_{t=1}=降伏変位\tag{9}\]
\[最大変位_{1<t}=\mathrm{max}\left(相対変位_t \,,\, 最大変位_{t-1}\right)\tag{10}\]
最大復元力(kN)
\[最大復元力_{t=1}=降伏耐力\tag{11}\]
\[最大復元力_{1<t}=\mathrm{max}\left(復元力_{t-1} \,,\, 最大復元力_{t-1}\right)\tag{12}\]
復元力(kN)
\[復元力_{t=1}=初期剛性\times相対変位_{t=1}\tag{13}\]
X0(m)
\[\mathrm{X0}_t=相対変位_{t-1}-復元力_{t-1}/初期剛性\tag{14}\]
Y1(kN)
\[\mathrm{Y1}_t=初期剛性\times(相対変位_t-\mathrm{X0}_t)\tag{15}\]
Y2(kN)
\[\mathrm{Y2}_t=(相対変位_t - \mathrm{X0}_t) \times \dfrac{最大復元力_t}{最大変位_t-\mathrm{X0}_t}\tag{16}\]
Y3(kN)
\[\mathrm{Y3}_t=(相対変位_t - \mathrm{X0}_t) \times \dfrac{最小復元力_t}{最小変位_t-\mathrm{X0}_t}\tag{17}\]
Y4(kN)
\[\mathrm{Y4}_t= 復元力_{t-1} + (最大復元力_t - 復元力_{t-1}) \times \dfrac{相対変位_t-相対変位_{t-1}}{最大変位_t-相対変位_{t-1}}\tag{18}\]
Y5(kN)
\[\mathrm{Y5}_t= 復元力_{t-1} + (復元力_{t-1} - 最小復元力_t) \times \dfrac{相対変位_t-相対変位_{t-1}}{相対変位_{t-1}-最小変位_t}\tag{19}\]
\[復元力_{1<t}=\begin{cases} 降伏耐力+(相対変位_t-降伏変位)\times二次剛性 & 相対変位_t \geq相対変位_{t-1}\,かつ\,相対変位_t>最大変位_{t-1}\\中央値\{\mathrm{Y1}_t,\mathrm{Y2}_t,\mathrm{Y4}_t\}&相対変位_t\geq相対変位_{t-1}\,かつ\,相対変位_t\leq 最大変位_{t-1}\\-降伏耐力+(相対変位_t+降伏変位)\times二次剛性&相対変位_t<相対変位_{t-1}\,かつ\,相対変位_t<最小変位_{t-1}\\中央値\{\mathrm{Y1}_t,\mathrm{Y3}_t,\mathrm{Y5}_t\}&相対変位_t<相対変位_{t-1}\,かつ\,相対変位_t\geq最小変位_{t-1}\end{cases}\tag{20}\]
調整外力(kN)
\[調整外力_t=初期剛性\times相対変位_t-復元力_t\tag{21}\]
調整外力の増分(kN)
\[調整外力の増分_t=調整外力_t-調整外力_{t-1}\tag{22}\]
相対速度(m/s)
\[質量+\Delta t\times \dfrac{粘性減衰係数}{2}\tag{23}\]
\[相対速度_t=-\,相対速度_{t-1}+\dfrac{2\times(相対変位_t-相対変位_{t-1})}{\Delta t}+\dfrac{調整外力の増分_t\times\Delta t}{2\times(23)}\tag{24}\]
相対加速度(m/s2)
\[相対加速度_t=-\,相対加速度_{t-1}-\dfrac{4\times相対速度_{t-1}}{\Delta t}+\dfrac{4\times(相対変位_t-相対変位_{t-1})}{\Delta t^2}+\dfrac{調整外力の増分_t}{(23)}\tag{25}\]
絶対加速度(m/s2)
\[絶対加速度_t=地震波_t+相対加速度_t\tag{26}\]
履歴エネルギー(kN・m)
\[履歴エネルギー_t=\dfrac{(復元力_t+復元力_{t-1})\times(相対変位_t-相対変位_{t-1})}{2}\tag{27}\]
入力エネルギー(kN・m)
\[入力エネルギー_t=-\dfrac{\left(地震波_{t-1}\times相対速度_{t-1}+地震波_{t}\times相対速度_{t}\right)\times\Delta t\times質量}{2}\tag{28}\]
累積履歴エネルギー吸収量(kN・m)
\[累積履歴エネルギー吸収量_t=履歴エネルギー_t+累積履歴エネルギー吸収量_{t-1}\tag{29}\]
累積入力エネルギー量(kN・m)
\[累積入力エネルギー量_t=入力エネルギー_t+累積入力エネルギー量_{t-1}\tag{30}\]
最大塑性率(-)
\[最大塑性率=最大応答変位\,\,/\,\,降伏変位\tag{31}\]
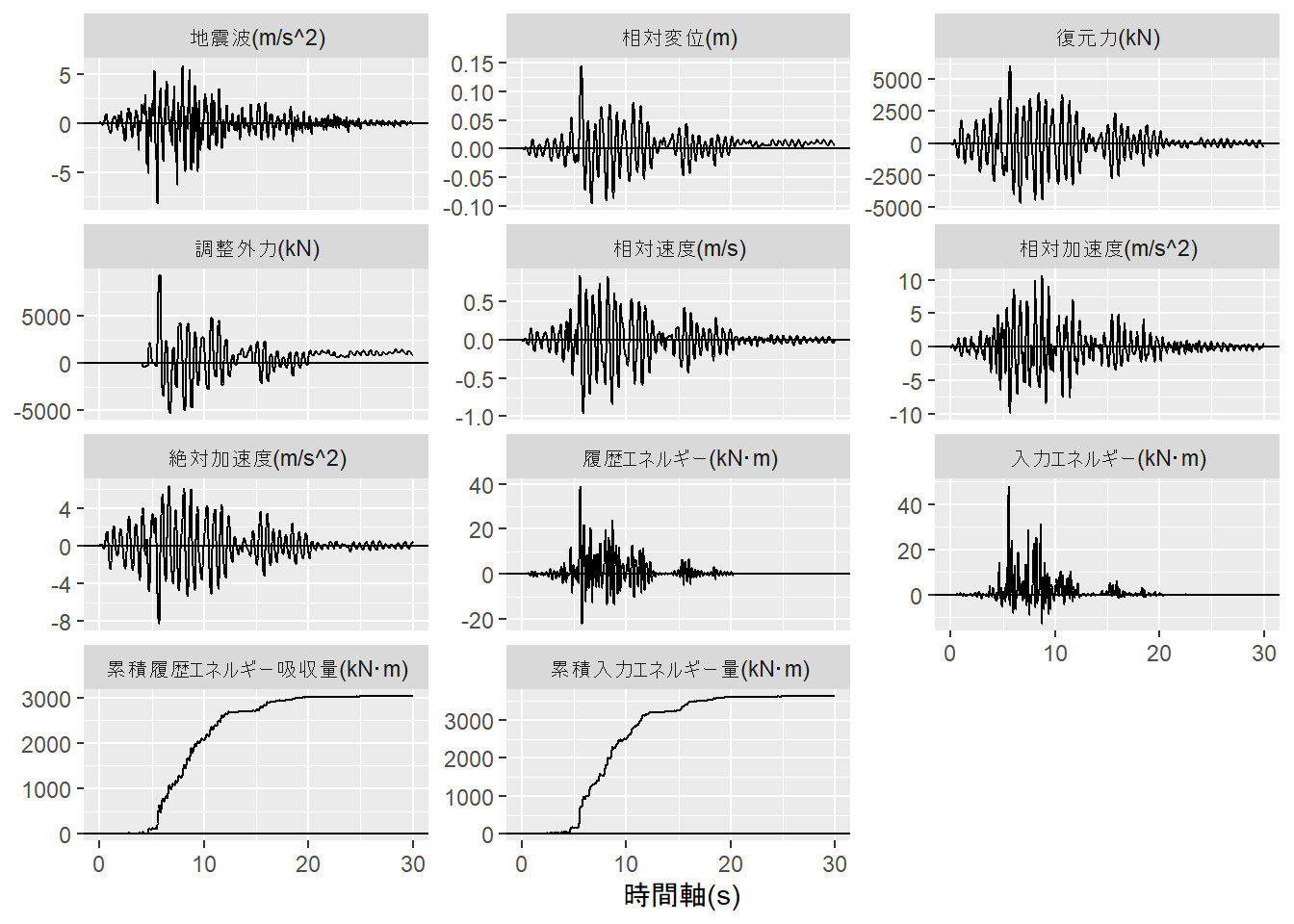
それではサンプル地震波に対する時間刻み毎の応答を求めます。Figure 2 が各種応答の推移です。
relative_displacement <-
minimum_displacement <-
minimum_restoring <-
maximal_displacement <-
maximal_restoring <-
X0 <- Y1 <- Y2 <- Y3 <- Y4 <- Y5 <-
median_y1y2y4 <-
median_y1y3y5 <-
restoring <-
external_force <-
external_force_diff <-
relative_velocity <-
relative_acceleration <-
absolute_acceleration <-
hysteretic_energy <-
input_energy <-
cumulative_hysteretic_energy_absorption <-
cumulative_input_energy <- rep(0, N)
# 式(3)
eq03 <- k1 + 2 * viscous_damping_coefficient / Delta_t + 4 * m / Delta_t^2
# 式(23)
eq23 <- m + Delta_t * viscous_damping_coefficient / 2
# 初期値
minimum_displacement[1] <- -delta_y # 式(5)
minimum_restoring[1] <- -Py # 式(7)
maximal_displacement[1] <- delta_y # 式(9)
maximal_restoring[1] <- Py # 式(11)
restoring[1] <- k1 * relative_displacement[1] # 式(13)
for (n in 2:N) {
# 相対変位 式(4)
term1 <- -m * earthquake_wave[n]
term2 <- external_force[n - 1]
# 式(1)
eq01_1 <- 4 * relative_displacement[n - 1] / Delta_t^2
eq01_2 <- 4 * relative_velocity[n - 1] / Delta_t
eq01_3 <- relative_acceleration[n - 1]
eq01 <- m * (eq01_1 + eq01_2 + eq01_3)
eq02 <- viscous_damping_coefficient * (2 * relative_displacement[n - 1] / Delta_t + relative_velocity[n - 1])
relative_displacement[n] <- (term1 + term2 + eq01 + eq02) / eq03
# 最小変位 式(6)
minimum_displacement[n] <- min(relative_displacement[n], minimum_displacement[n - 1])
# 最小復元力 式(8)
minimum_restoring[n] <- min(restoring[n - 1], minimum_restoring[n - 1])
# 最大変位 式(10)
maximal_displacement[n] <- max(relative_displacement[n], maximal_displacement[n - 1])
# 最大復元力 式(12)
maximal_restoring[n] <- max(restoring[n - 1], maximal_restoring[n - 1])
# 復元力 式(20)
X0[n] <- relative_displacement[n - 1] - restoring[n - 1] / k1 # 式(14)
Y1[n] <- k1 * (relative_displacement[n] - X0[n]) # 式(15)
Y2[n] <- (relative_displacement[n] - X0[n]) * maximal_restoring[n] / (maximal_displacement[n] - X0[n]) # 式(16)
Y3[n] <- (relative_displacement[n] - X0[n]) * minimum_restoring[n] / (minimum_displacement[n] - X0[n]) # 式(17)
Y4[n] <- restoring[n - 1] + (maximal_restoring[n] - restoring[n - 1]) * (relative_displacement[n] - relative_displacement[n - 1]) / (maximal_displacement[n] - relative_displacement[n - 1]) # 式(18)
Y5[n] <- restoring[n - 1] + (restoring[n - 1] - minimum_restoring[n]) * (relative_displacement[n] - relative_displacement[n - 1]) / (relative_displacement[n - 1] - minimum_displacement[n]) # 式(19)
median_y1y2y4[n] <- median(c(Y1[n], Y2[n], Y4[n]))
median_y1y3y5[n] <- median(c(Y1[n], Y3[n], Y5[n]))
if (relative_displacement[n] >= relative_displacement[n - 1]) {
if (relative_displacement[n] > maximal_displacement[n - 1]) {
restoring[n] <- Py + (relative_displacement[n] - delta_y) * k2
} else {
restoring[n] <- median_y1y2y4[n]
}
} else {
if (relative_displacement[n] < minimum_displacement[n - 1]) {
restoring[n] <- -Py + (relative_displacement[n] + delta_y) * k2
} else {
restoring[n] <- median_y1y3y5[n]
}
}
# 調整外力 式(21)
external_force[n] <- k1 * relative_displacement[n] - restoring[n]
# 調整外力の増分 式(22)
external_force_diff[n] <- external_force[n] - external_force[n - 1]
# 相対速度 式(24)
relative_velocity[n] <- -1 * relative_velocity[n - 1] + 2 * (relative_displacement[n] - relative_displacement[n - 1]) / Delta_t + external_force_diff[n] * Delta_t / 2 / eq23
# 相対加速度 式(25)
relative_acceleration[n] <- -1 * relative_acceleration[n - 1] - 4 * relative_velocity[n - 1] / Delta_t + 4 * (relative_displacement[n] - relative_displacement[n - 1]) / Delta_t^2 + external_force_diff[n] / eq23
# 履歴エネルギー 式(27)
hysteretic_energy[n] <- (restoring[n] + restoring[n - 1]) * (relative_displacement[n] - relative_displacement[n - 1]) / 2
# 入力エネルギー 式(28)
input_energy[n] <- -1 * (earthquake_wave[n - 1] * relative_velocity[n - 1] + earthquake_wave[n] * relative_velocity[n]) * Delta_t / 2 * m
# 累積履歴エネルギー吸収量 式(29)
cumulative_hysteretic_energy_absorption[n] <- hysteretic_energy[n] + cumulative_hysteretic_energy_absorption[n - 1]
# 累積入力エネルギー量 式(30)
cumulative_input_energy[n] <- input_energy[n] + cumulative_input_energy[n - 1]
}
# 絶対加速度 式(26)
absolute_acceleration <- earthquake_wave + relative_accelerationdfresponse <-
data.frame(
T,
earthquake_wave,
relative_displacement,
restoring,
external_force,
relative_velocity,
relative_acceleration,
absolute_acceleration,
hysteretic_energy,
input_energy,
cumulative_hysteretic_energy_absorption,
cumulative_input_energy
)
colnames(dfresponse) <-
c(
"時間軸(s)",
"地震波(m/s^2)",
"相対変位(m)",
"復元力(kN)",
"調整外力(kN)",
"相対速度(m/s)",
"相対加速度(m/s^2)",
"絶対加速度(m/s^2)",
"履歴エネルギー(kN・m)",
"入力エネルギー(kN・m)",
"累積履歴エネルギー吸収量(kN・m)",
"累積入力エネルギー量(kN・m)"
)
tidyresponse <- dfresponse %>% tidyr::gather(key = "key", value = "value", colnames(.)[-1])
tidyresponse$key <- tidyresponse$key %>% factor(levels = unique(.))
tidyresponse %>% ggplot(mapping = aes(x = `時間軸(s)`, y = value)) +
geom_line() +
facet_wrap(. ~ key, scale = "free_y", ncol = 3) +
theme(axis.title.y = element_blank()) +
geom_hline(yintercept = 0)最後に各応答の最大値を確認します。
list(
`最大応答加速度(m/s^2)` = max(abs(absolute_acceleration)),
`最大応答変位(m)` = max(abs(relative_displacement)),
`最大応答速度(m/s)` = max(abs(relative_velocity)),
`最大復元力(kN)` = max(abs(restoring)),
`最大塑性率(-)` = max(abs(relative_displacement)) / delta_y
)$`最大応答加速度(m/s^2)`
[1] 8.256843
$`最大応答変位(m)`
[1] 0.1454733
$`最大応答速度(m/s)`
[1] 0.960762
$`最大復元力(kN)`
[1] 6091.285
$`最大塑性率(-)`
[1] 5.489557以上です。