Rを利用してロバスト標準誤差を求めます。
本ページは以下の資料を引用参照しています。
- https://economics.mit.edu/sites/default/files/2022-09/Heteroskedasticity-Robust%20Inference%20In%20Finite%20Samples.pdf
- Cribari-Neto, F., Souza, T. C., & Vasconcellos, K. L. P. (2007). Inference Under Heteroskedasticity and Leveraged Data. Communications in Statistics - Theory and Methods, 36(10), 1877–1888.
- https://www.tandfonline.com/doi/full/10.1080/03610920802109210
- https://danielbaissa.com/intro_to_stats/robust-standard-errors-tackling-heteroscedasticity
- https://py4etrics.github.io/14_Hetero.html
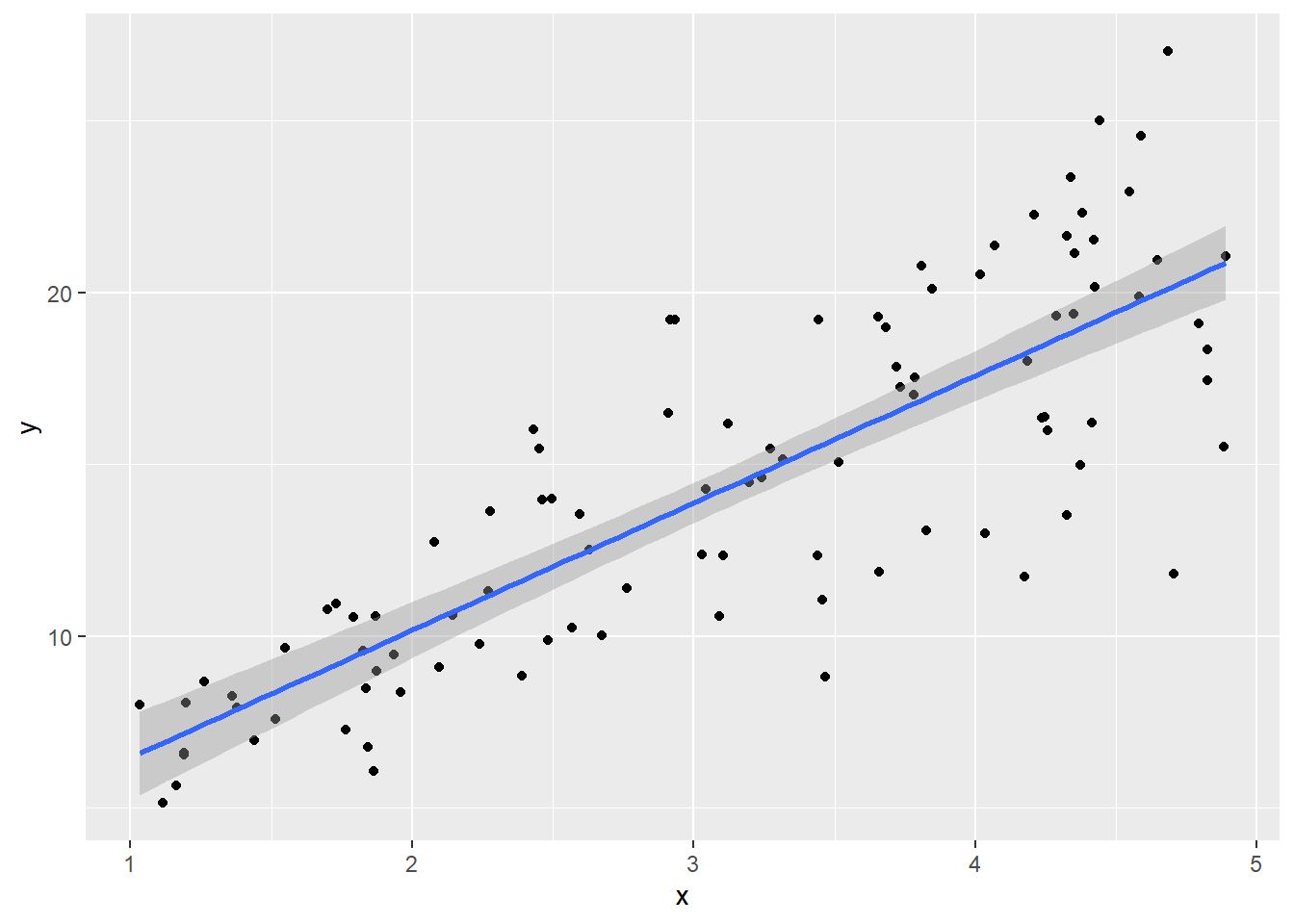
始めに共通して利用する「残差の分散が不均一」なサンプルデータを作成します。ここでは昇順にソートした説明変数(x)を標準偏差とした正規分布を残差として従属変数(y)を作成します。
library(dplyr)
library(ggplot2)
seed <- 20250115
set.seed(seed = seed)
n <- 100
x <- runif(n = n, min = 1, max = 5) %>% sort()
X <- cbind(1, x)
beta_true <- c(2, 4)
errors <- rnorm(n, sd = x)
y <- X %*% beta_true + errors
ggplot(mapping = aes(x = x, y = y)) +
geom_point() +
geom_smooth(method = "lm")OLS推定の結果です。
# OLS推定
beta_hat <- solve(t(X) %*% X) %*% t(X) %*% y
# 残差の計算
residuals <- (y - X %*% beta_hat) %>% as.vector()推定された係数
beta_hat [,1]
2.759427
x 3.703825残差の基本統計量
summary(residuals) Min. 1st Qu. Median Mean 3rd Qu. Max.
-8.3806 -1.9492 0.1166 0.0000 2.0006 6.8978 参考として lm{stats} を利用した結果です。
lm(y ~ x) %>% summary()
Call:
lm(formula = y ~ x)
Residuals:
Min 1Q Median 3Q Max
-8.3806 -1.9492 0.1166 2.0006 6.8978
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2.7594 0.8530 3.235 0.00166 **
x 3.7038 0.2564 14.446 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 2.942 on 98 degrees of freedom
Multiple R-squared: 0.6805, Adjusted R-squared: 0.6772
F-statistic: 208.7 on 1 and 98 DF, p-value: < 2.2e-16続いて分散共分散行列、標準誤差、95%信頼区間を非ロバスト、HC0、HC1、HC2、HC3、HC4、HC5それぞれについて求めます。
\[\Sigma=\hat{\sigma}^2 \left(X^{'}X\right)^{-1}\] 非ロバストな分散共分散、標準誤差および95%信頼区間を求めます。左から2列目までが分散共分散行列、3列目が標準誤差、4列目は信頼区間下限、5列目は信頼区間上限です。
# 残差平方和の計算
RSS <- sum(residuals^2)
# 自由度 (n - k)
k <- ncol(X)
df <- n - k
# 誤差分散の推定
sigma2_hat <- RSS / df
# 共分散行列の計算
var_beta_hat <- sigma2_hat * solve(t(X) %*% X)
# 標準誤差の計算
se_beta_hat <- sqrt(diag(var_beta_hat))
# 95%信頼区間の計算
alpha <- 0.05
critical_value <- qt(1 - alpha / 2, df) # t分布の臨界値
lower_ci <- beta_hat - critical_value * se_beta_hat # 下限
upper_ci <- beta_hat + critical_value * se_beta_hat # 上限
# 結果のまとめ
result_no_robust <- data.frame(var_beta_hat, se_beta_hat, lower_ci, upper_ci, check.names = F)
colnames(result_no_robust)[1] <- "(Intercept)"
row.names(result_no_robust)[1] <- "(Intercept)"
result_no_robust (Intercept) x se_beta_hat lower_ci upper_ci
(Intercept) 0.7276829 -0.20528850 0.8530433 1.066590 4.452263
x -0.2052885 0.06573337 0.2563852 3.195037 4.212613参考として confint{stats} を利用して95%信頼区間を求めます。
lm(y ~ x) %>% confint(level = .95) 2.5 % 97.5 %
(Intercept) 1.066590 4.452263
x 3.195037 4.212613\[\begin{eqnarray} y&=&X\beta+u,\quad\Sigma=\left(X^{'}X\right)^{-1}X^{'}\Omega X \left(X^{'}X\right)^{-1}\\ \Omega&=&\textrm{diag}\{\hat{u}_i^2\} \end{eqnarray}\]
調整をHC0としたロバストな分散共分散、標準誤差および95%信頼区間を求めます。左から2列目までが分散共分散行列、3列目が標準誤差、4列目は信頼区間下限、5列目は信頼区間上限です。
# HC0共分散行列の計算
vcov_HC0 <- solve(t(X) %*% X) %*% (t(X) %*% diag(residuals^2) %*% X) %*% solve(t(X) %*% X)
# 標準誤差の計算
robust_se_HC0 <- sqrt(diag(vcov_HC0))
# 95%信頼区間の計算
lower_ci_HC0 <- beta_hat - critical_value * robust_se_HC0
upper_ci_HC0 <- beta_hat + critical_value * robust_se_HC0
# 結果のまとめ
result_robust_HC0 <- data.frame(vcov_HC0, robust_se_HC0, lower_ci_HC0, upper_ci_HC0, check.names = F)
colnames(result_robust_HC0)[1] <- "(Intercept)"
row.names(result_robust_HC0)[1] <- "(Intercept)"
result_robust_HC0 (Intercept) x robust_se_HC0 lower_ci_HC0 upper_ci_HC0
(Intercept) 0.4127924 -0.1460259 0.6424893 1.484428 4.034426
x -0.1460259 0.0598892 0.2447227 3.218181 4.189469参考として vcovHC{plm} と coeftest{lmtest} を利用して分散共分散行列と95%信頼区間を求めます。
vcov_HC0 <- plm::vcovHC(lm(y ~ x), type = "HC0")
model_HC0 <- vcov_HC0 %>% lmtest::coeftest(lm(y ~ x), .)
robust_se_HC0 <- model_HC0[, "Std. Error"]
ci_HC0 <- model_HC0 %>% stats::confint()
list(分散共分散行列_HC0 = vcov_HC0, 標準誤差_HC0 = robust_se_HC0, 信頼区間_HC0 = ci_HC0)$分散共分散行列_HC0
(Intercept) x
(Intercept) 0.4127924 -0.1460259
x -0.1460259 0.0598892
$標準誤差_HC0
(Intercept) x
0.6424893 0.2447227
$信頼区間_HC0
2.5 % 97.5 %
(Intercept) 1.484428 4.034426
x 3.218181 4.189469\[\begin{eqnarray} y&=&X\beta+u,\quad\Sigma=\left(X^{'}X\right)^{-1}X^{'}\Omega X\left(X^{'}X\right)^{-1}\\ \Omega&=&\dfrac{n}{n-k}\,\textrm{diag}\left\{\hat{u}_i^2\right\} \end{eqnarray}\]
調整をHC1としたロバストな分散共分散、標準誤差および95%信頼区間を求めます。左から2列目までが分散共分散行列、3列目が標準誤差、4列目は信頼区間下限、5列目は信頼区間上限です。
# HC1共分散行列の計算
vcov_HC1 <- (n / (n - k)) * solve(t(X) %*% X) %*% (t(X) %*% diag(residuals^2) %*% X) %*% solve(t(X) %*% X)
# 標準誤差の計算
robust_se_HC1 <- sqrt(diag(vcov_HC1))
# 95%信頼区間の計算
lower_ci_HC1 <- beta_hat - critical_value * robust_se_HC1
upper_ci_HC1 <- beta_hat + critical_value * robust_se_HC1
# 結果のまとめ
result_robust_HC1 <- data.frame(vcov_HC1, robust_se_HC1, lower_ci_HC1, upper_ci_HC1, check.names = F)
colnames(result_robust_HC1)[1] <- "(Intercept)"
row.names(result_robust_HC1)[1] <- "(Intercept)"
result_robust_HC1 (Intercept) x robust_se_HC1 lower_ci_HC1 upper_ci_HC1
(Intercept) 0.4212168 -0.14900601 0.6490122 1.471483 4.04737
x -0.1490060 0.06111143 0.2472073 3.213250 4.19440参考として vcovHC{plm} と coeftest{lmtest} を利用して分散共分散行列と95%信頼区間を求めます。
vcov_HC1 <- plm::vcovHC(lm(y ~ x), type = "HC1")
model_HC1 <- vcov_HC1 %>% lmtest::coeftest(lm(y ~ x), .)
robust_se_HC1 <- model_HC1[, "Std. Error"]
ci_HC1 <- model_HC1 %>% stats::confint()
list(分散共分散行列_HC1 = vcov_HC1, 標準誤差_HC1 = robust_se_HC1, 信頼区間_HC1 = ci_HC1)$分散共分散行列_HC1
(Intercept) x
(Intercept) 0.4212168 -0.14900601
x -0.1490060 0.06111143
$標準誤差_HC1
(Intercept) x
0.6490122 0.2472073
$信頼区間_HC1
2.5 % 97.5 %
(Intercept) 1.471483 4.04737
x 3.213250 4.19440\[\begin{eqnarray} y&=&X\beta+u,\quad \Sigma=\left(X^{'}X\right)^{-1}X^{'}\Omega X\left(X^{'}X\right)^{-1}\\ \Omega&=&\textrm{diag}\left\{\dfrac{\hat{u}_i^2}{1-h_i}\right\},\quad h=\textrm{diag}\left\{X\left(X^{'}X\right)^{-1}X^{'}\right\} \end{eqnarray}\]
調整をHC2としたロバストな分散共分散、標準誤差および95%信頼区間を求めます。左から2列目までが分散共分散行列、3列目が標準誤差、4列目は信頼区間下限、5列目は信頼区間上限です。
# ハット行列の計算
H <- X %*% solve(t(X) %*% X) %*% t(X)
leverage <- diag(H)
# HC2共分散行列の計算
vcov_HC2 <- solve(t(X) %*% X) %*% (t(X) %*% diag(residuals^2 / (1 - leverage)) %*% X) %*% solve(t(X) %*% X)
# 標準誤差の計算
robust_se_HC2 <- sqrt(diag(vcov_HC2))
# 95%信頼区間の計算
lower_ci_HC2 <- beta_hat - critical_value * robust_se_HC2
upper_ci_HC2 <- beta_hat + critical_value * robust_se_HC2
# 結果のまとめ
result_robust_HC2 <- data.frame(vcov_HC2, robust_se_HC2, lower_ci_HC2, upper_ci_HC2, check.names = F)
colnames(result_robust_HC2)[1] <- "(Intercept)"
row.names(result_robust_HC2)[1] <- "(Intercept)"
result_robust_HC2 (Intercept) x robust_se_HC2 lower_ci_HC2 upper_ci_HC2
(Intercept) 0.4232785 -0.14987214 0.6505986 1.468335 4.050518
x -0.1498721 0.06144887 0.2478888 3.211898 4.195753参考として vcovHC{plm} と coeftest{lmtest} を利用して分散共分散行列と95%信頼区間を求めます。
vcov_HC2 <- plm::vcovHC(lm(y ~ x), type = "HC2")
model_HC2 <- vcov_HC2 %>% lmtest::coeftest(lm(y ~ x), .)
robust_se_HC2 <- model_HC2[, "Std. Error"]
ci_HC2 <- model_HC2 %>% stats::confint()
list(分散共分散行列_HC2 = vcov_HC2, 標準誤差_HC2 = robust_se_HC2, 信頼区間_HC2 = ci_HC2)$分散共分散行列_HC2
(Intercept) x
(Intercept) 0.4232785 -0.14987214
x -0.1498721 0.06144887
$標準誤差_HC2
(Intercept) x
0.6505986 0.2478888
$信頼区間_HC2
2.5 % 97.5 %
(Intercept) 1.468335 4.050518
x 3.211898 4.195753\[\begin{eqnarray} y&=&X\beta+u,\quad \Sigma=\left(X^{'}X\right)^{-1}X^{'}\Omega X\left(X^{'}X\right)^{-1}\\ \Omega&=&\textrm{diag}\left\{\left(\dfrac{\hat{u}_i}{1-h_i}\right)^2\right\},\quad h=\textrm{diag}\left\{X\left(X^{'}X\right)^{-1}X^{'}\right\} \end{eqnarray}\]
調整をHC3としたロバストな分散共分散、標準誤差および95%信頼区間を求めます。左から2列目までが分散共分散行列、3列目が標準誤差、4列目は信頼区間下限、5列目は信頼区間上限です。
# ハット行列の計算
H <- X %*% solve(t(X) %*% X) %*% t(X)
leverage <- diag(H)
# HC3共分散行列の計算
vcov_HC3 <- solve(t(X) %*% X) %*% (t(X) %*% diag(residuals^2 / (1 - leverage)^2) %*% X) %*% solve(t(X) %*% X)
# 標準誤差の計算
robust_se_HC3 <- sqrt(diag(vcov_HC3))
# 95%信頼区間の計算
lower_ci_HC3 <- beta_hat - critical_value * robust_se_HC3
upper_ci_HC3 <- beta_hat + critical_value * robust_se_HC3
# 結果のまとめ
result_robust_HC3 <- data.frame(vcov_HC3, robust_se_HC3, lower_ci_HC3, upper_ci_HC3, check.names = F)
colnames(result_robust_HC3)[1] <- "(Intercept)"
row.names(result_robust_HC3)[1] <- "(Intercept)"
result_robust_HC3 (Intercept) x robust_se_HC3 lower_ci_HC3 upper_ci_HC3
(Intercept) 0.4340587 -0.15382702 0.6588313 1.451997 4.066856
x -0.1538270 0.06305187 0.2511013 3.205523 4.202128参考として vcovHC{plm} と coeftest{lmtest} を利用して分散共分散行列と95%信頼区間を求めます。
vcov_HC3 <- plm::vcovHC(lm(y ~ x), type = "HC3")
model_HC3 <- vcov_HC3 %>% lmtest::coeftest(lm(y ~ x), .)
robust_se_HC3 <- model_HC3[, "Std. Error"]
ci_HC3 <- model_HC3 %>% stats::confint()
list(分散共分散行列_HC3 = vcov_HC3, 標準誤差_HC3 = robust_se_HC3, 信頼区間_HC3 = ci_HC3)$分散共分散行列_HC3
(Intercept) x
(Intercept) 0.4340587 -0.15382702
x -0.1538270 0.06305187
$標準誤差_HC3
(Intercept) x
0.6588313 0.2511013
$信頼区間_HC3
2.5 % 97.5 %
(Intercept) 1.451997 4.066856
x 3.205523 4.202128\[\begin{eqnarray} y&=&X\beta+u,\quad \Sigma=\left(X^{'}X\right)^{-1}X^{'}\Omega X\left(X^{'}X\right)^{-1}\\ \Omega&=&\textrm{diag}\left\{\dfrac{\hat{u}_i^2}{(1-h_i)^{\delta_i}}\right\},\quad h=\textrm{diag}\left\{X\left(X^{'}X\right)^{-1}X^{'}\right\}\\ \delta_i&=&\textrm{min}\left\{4,nh_i/k\right\} \end{eqnarray}\]
調整をHC4としたロバストな分散共分散、標準誤差および95%信頼区間を求めます。左から2列目までが分散共分散行列、3列目が標準誤差、4列目は信頼区間下限、5列目は信頼区間上限です。
# ハット行列の計算
H <- X %*% solve(t(X) %*% X) %*% t(X)
leverage <- diag(H)
# HC4共分散行列の計算
delta <- pmin(4, n * leverage / k)
weights <- 1 / (1 - leverage)^delta
vcov_HC4 <- solve(t(X) %*% X) %*% (t(X) %*% diag(residuals^2 * weights) %*% X) %*% solve(t(X) %*% X)
# 標準誤差の計算
robust_se_HC4 <- sqrt(diag(vcov_HC4))
# 95%信頼区間の計算
lower_ci_HC4 <- beta_hat - critical_value * robust_se_HC4
upper_ci_HC4 <- beta_hat + critical_value * robust_se_HC4
# 結果のまとめ
result_robust_HC4 <- data.frame(vcov_HC4, robust_se_HC4, lower_ci_HC4, upper_ci_HC4, check.names = F)
colnames(result_robust_HC4)[1] <- "(Intercept)"
row.names(result_robust_HC4)[1] <- "(Intercept)"
result_robust_HC4 (Intercept) x robust_se_HC4 lower_ci_HC4 upper_ci_HC4
(Intercept) 0.4271849 -0.15134041 0.6535939 1.462391 4.056462
x -0.1513404 0.06200895 0.2490160 3.209661 4.197989参考として vcovHC{plm} と coeftest{lmtest} を利用して分散共分散行列と95%信頼区間を求めます。
vcov_HC4 <- plm::vcovHC(lm(y ~ x), type = "HC4")
model_HC4 <- vcov_HC4 %>% lmtest::coeftest(lm(y ~ x), .)
robust_se_HC4 <- model_HC4[, "Std. Error"]
ci_HC4 <- model_HC4 %>% stats::confint()
list(分散共分散行列_HC4 = vcov_HC4, 標準誤差_HC4 = robust_se_HC4, 信頼区間_HC4 = ci_HC4)$分散共分散行列_HC4
(Intercept) x
(Intercept) 0.4271849 -0.15134041
x -0.1513404 0.06200895
$標準誤差_HC4
(Intercept) x
0.6535939 0.2490160
$信頼区間_HC4
2.5 % 97.5 %
(Intercept) 1.462391 4.056462
x 3.209661 4.197989\[\begin{eqnarray} y&=&X\beta+u,\quad \Sigma=\left(X^{'}X\right)^{-1}X^{'}\Omega X\left(X^{'}X\right)^{-1}\\ \Omega&=&\textrm{diag}\left\{\dfrac{\hat{u}_i^2}{\sqrt{(1-h_i)^{\alpha_i}}}\right\},\quad h=\textrm{diag}\left\{X\left(X^{'}X\right)^{-1}X^{'}\right\}\\ \alpha_i&=&\textrm{min}\left\{\dfrac{nh_i}{p},\max\left\{4,\dfrac{n\,k\,h_{max}}{p}\right\}\right\}\\ p&=&\displaystyle\sum_{i=1}^nh_i \end{eqnarray}\]
調整をHC5としたロバストな分散共分散、標準誤差および95%信頼区間を求めます。左から2列目までが分散共分散行列、3列目が標準誤差、4列目は信頼区間下限、5列目は信頼区間上限です。
# ハット行列の計算
H <- X %*% solve(t(X) %*% X) %*% t(X)
leverage <- diag(H)
p <- sum(leverage)
# HC5共分散行列の計算
k <- 0.7
alpha <- pmin(n * leverage / p, pmax(4, n * k * max(leverage) / p))
weights <- 1 / sqrt((1 - leverage)^alpha)
vcov_HC5 <- solve(t(X) %*% X) %*% (t(X) %*% diag(residuals^2 * weights) %*% X) %*% solve(t(X) %*% X)
# 標準誤差の計算
robust_se_HC5 <- sqrt(diag(vcov_HC5))
# 95%信頼区間の計算
lower_ci_HC5 <- beta_hat - critical_value * robust_se_HC5
upper_ci_HC5 <- beta_hat + critical_value * robust_se_HC5
# 結果のまとめ
result_robust_HC5 <- data.frame(vcov_HC5, robust_se_HC5, lower_ci_HC5, upper_ci_HC5, check.names = F)
colnames(result_robust_HC5)[1] <- "(Intercept)"
row.names(result_robust_HC5)[1] <- "(Intercept)"
result_robust_HC5 (Intercept) x robust_se_HC5 lower_ci_HC5 upper_ci_HC5
(Intercept) 0.4199052 -0.14865332 0.6480009 1.473490 4.045363
x -0.1486533 0.06093771 0.2468556 3.213948 4.193702参考として vcovHC{plm} と coeftest{lmtest} を利用して分散共分散行列と95%信頼区間を求めます。
vcov_HC5 <- sandwich::vcovHC(lm(y ~ x), type = "HC5")
model_HC5 <- vcov_HC5 %>% lmtest::coeftest(lm(y ~ x), .)
robust_se_HC5 <- model_HC5[, "Std. Error"]
ci_HC5 <- model_HC5 %>% stats::confint()
list(分散共分散行列_HC5 = vcov_HC5, 標準誤差_HC5 = robust_se_HC5, 信頼区間_HC5 = ci_HC5)$分散共分散行列_HC5
(Intercept) x
(Intercept) 0.4199052 -0.14865332
x -0.1486533 0.06093771
$標準誤差_HC5
(Intercept) x
0.6480009 0.2468556
$信頼区間_HC5
2.5 % 97.5 %
(Intercept) 1.473490 4.045363
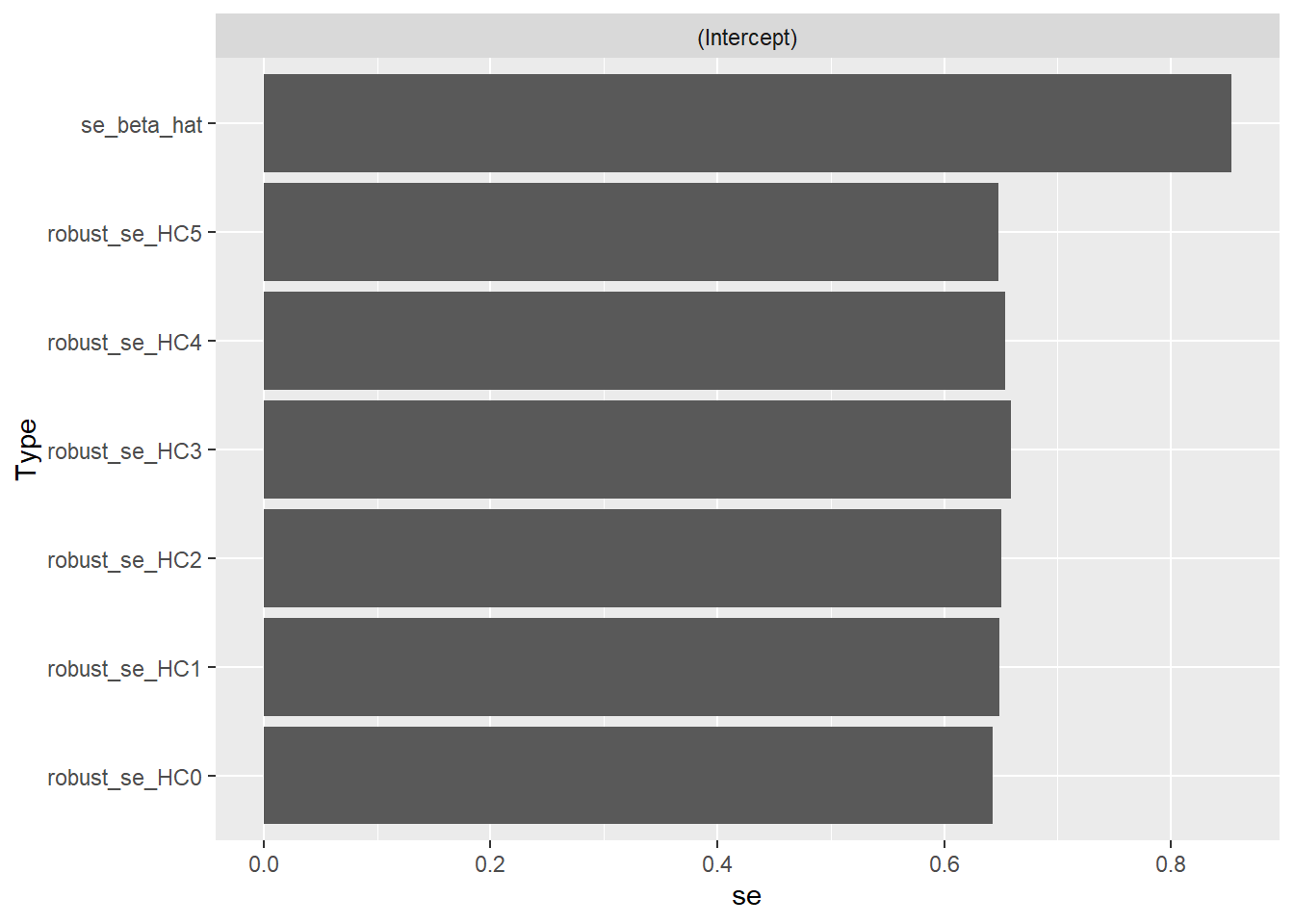
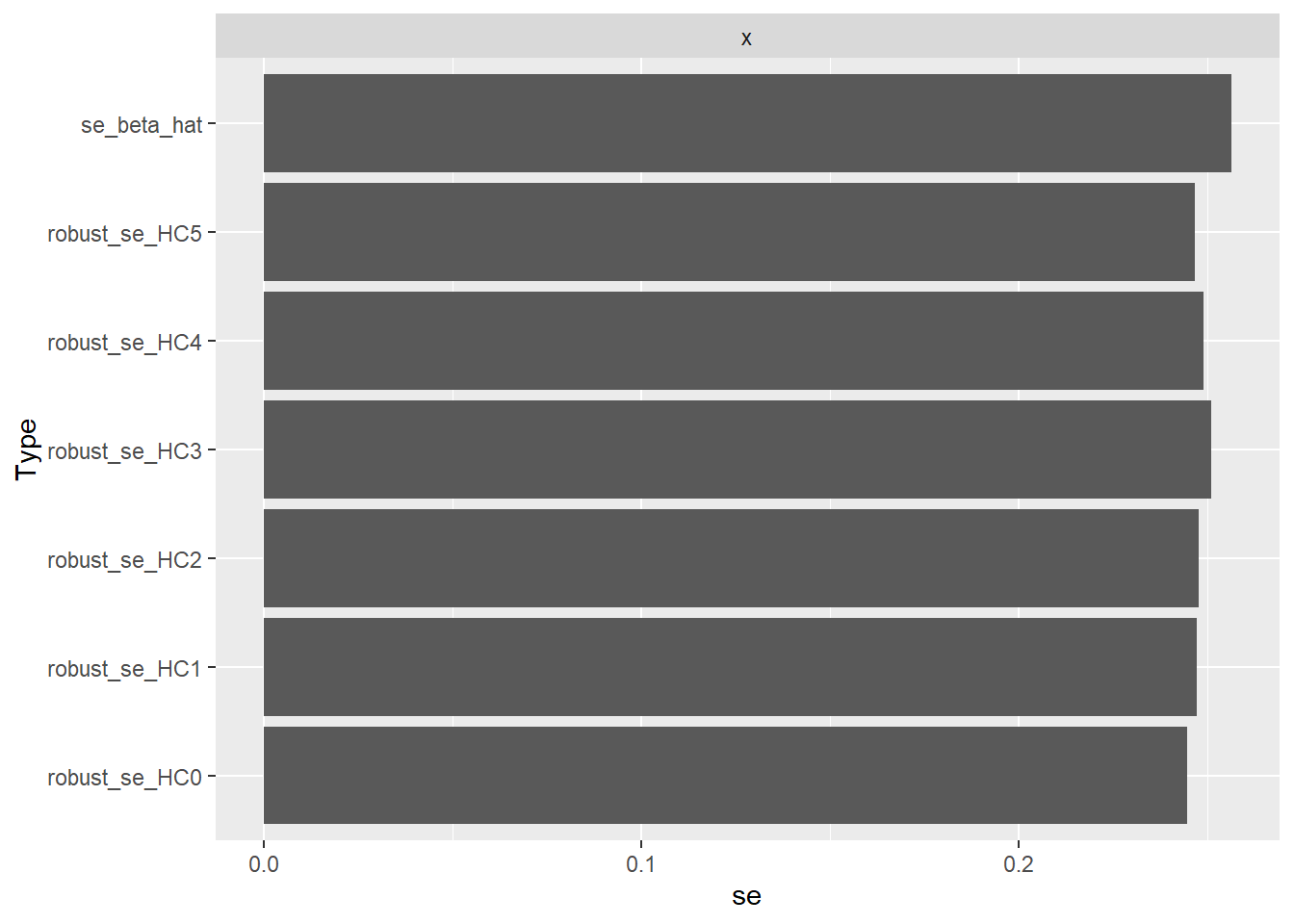
x 3.213948 4.193702推定された Intercept と x それぞれの標準誤差を比較します。
Intercept
fun_extract <- function(resultdf, n_row = 1, n_col = 3) {
df0 <- data.frame()
df0[1, 1] <- colnames(resultdf)[n_col]
df0[1, 2] <- resultdf[n_row, n_col]
colnames(df0) <- c("Type", row.names(resultdf)[n_row])
return(df0)
}
(dfcompare <- list(result_no_robust, result_robust_HC0, result_robust_HC1, result_robust_HC2, result_robust_HC3, result_robust_HC4, result_robust_HC5) %>% lapply(FUN = function(x) fun_extract(x)) %>% Reduce(function(x, y) rbind(x, y), .))
dfcompare %>%
tidyr::gather(, , colnames(.)[-1]) %>%
ggplot(mapping = aes(x = Type, y = value)) +
geom_bar(stat = "identity") +
facet_wrap(. ~ key) +
labs(y = "se") +
coord_flip() Type (Intercept)
1 se_beta_hat 0.8530433
2 robust_se_HC0 0.6424893
3 robust_se_HC1 0.6490122
4 robust_se_HC2 0.6505986
5 robust_se_HC3 0.6588313
6 robust_se_HC4 0.6535939
7 robust_se_HC5 0.6480009x
(dfcompare <- list(result_no_robust, result_robust_HC0, result_robust_HC1, result_robust_HC2, result_robust_HC3, result_robust_HC4, result_robust_HC5) %>% lapply(FUN = function(x) fun_extract(x, n_row = 2)) %>% Reduce(function(x, y) rbind(x, y), .))
dfcompare %>%
tidyr::gather(, , colnames(.)[-1]) %>%
ggplot(mapping = aes(x = Type, y = value)) +
geom_bar(stat = "identity") +
facet_wrap(. ~ key) +
labs(y = "se") +
coord_flip() Type x
1 se_beta_hat 0.2563852
2 robust_se_HC0 0.2447227
3 robust_se_HC1 0.2472073
4 robust_se_HC2 0.2478888
5 robust_se_HC3 0.2511013
6 robust_se_HC4 0.2490160
7 robust_se_HC5 0.2468556以上です。