RでBrunner-Munzel検定を行います。
以降の数式、導出は以下の資料を参照引用しています。
- Brunner, E., & Munzel, U. (2000). The Nonparametric Behrens-Fisher Problem: Asymptotic Theory and a Small-Sample Approximation. Biometrical Journal, 42(1), 17–25.
- https://corvus-window.com/excel_brunner-munzel/
- https://github.com/toshi-ara/brunnermunzel
- http://labs.kbs.keio.ac.jp/naoki50lab/nonparam2.pdf
- https://real-statistics.com/non-parametric-tests/brunner-munzel-test/
- https://www.jstage.jst.go.jp/article/psj/advpub/0/advpub_30.006/_pdf
- https://cran.r-project.org/web/packages/TOSTER/TOSTER.pdf
ブルンナー・ムンツェル検定では,2群の確率変数の分布に関する前提をおかず,各群から 1つずつサンプルを取り出したとき,どちらかが他方よりも大きくはならない確率をそれぞれ求め,それが 0.5 となるという帰無仮説を検定することを考える.つまり, \[p = \textrm{Prob}(X_A < X_B) + \dfrac{1}{2}\textrm{Prob}(X_A = X_B) \tag{1}\] において,p = 1/2 となるという仮説を検定する.
出所:http://labs.kbs.keio.ac.jp/naoki50lab/nonparam2.pdf
The BM test is designed to test the (two-sided) null hypothesis: \[\textrm{H}_0: \textrm{P}(x < y) = \textrm{P}(y < x) \tag{2}\] This hypothesis is called stochastic equality.
出所:https://real-statistics.com/non-parametric-tests/brunner-munzel-test/
As noted previously, the MW test is the nonparametric version of the t-test with equal variances and the BM test is the nonparametric version of the t-test with unequal variances.
出所:https://real-statistics.com/non-parametric-tests/brunner-munzel-test/
This tests the hypothesis that the relative effect, discussed below, is equal to the null value (default is mu = 0.5).The estimate of the relative effect, which can be considered as value similar to the probability of superiority, refers to the following: \[\hat{p} = p(X < Y ) + \dfrac{1}{2}\cdot P(X = Y ) \tag{3}\]
出所:https://cran.r-project.org/web/packages/TOSTER/TOSTER.pdf
サンプルとする2群のベクトルを作成します。
library(dplyr)
library(ggplot2)
set.seed(20250106)
n1 <- 25
n2 <- 35
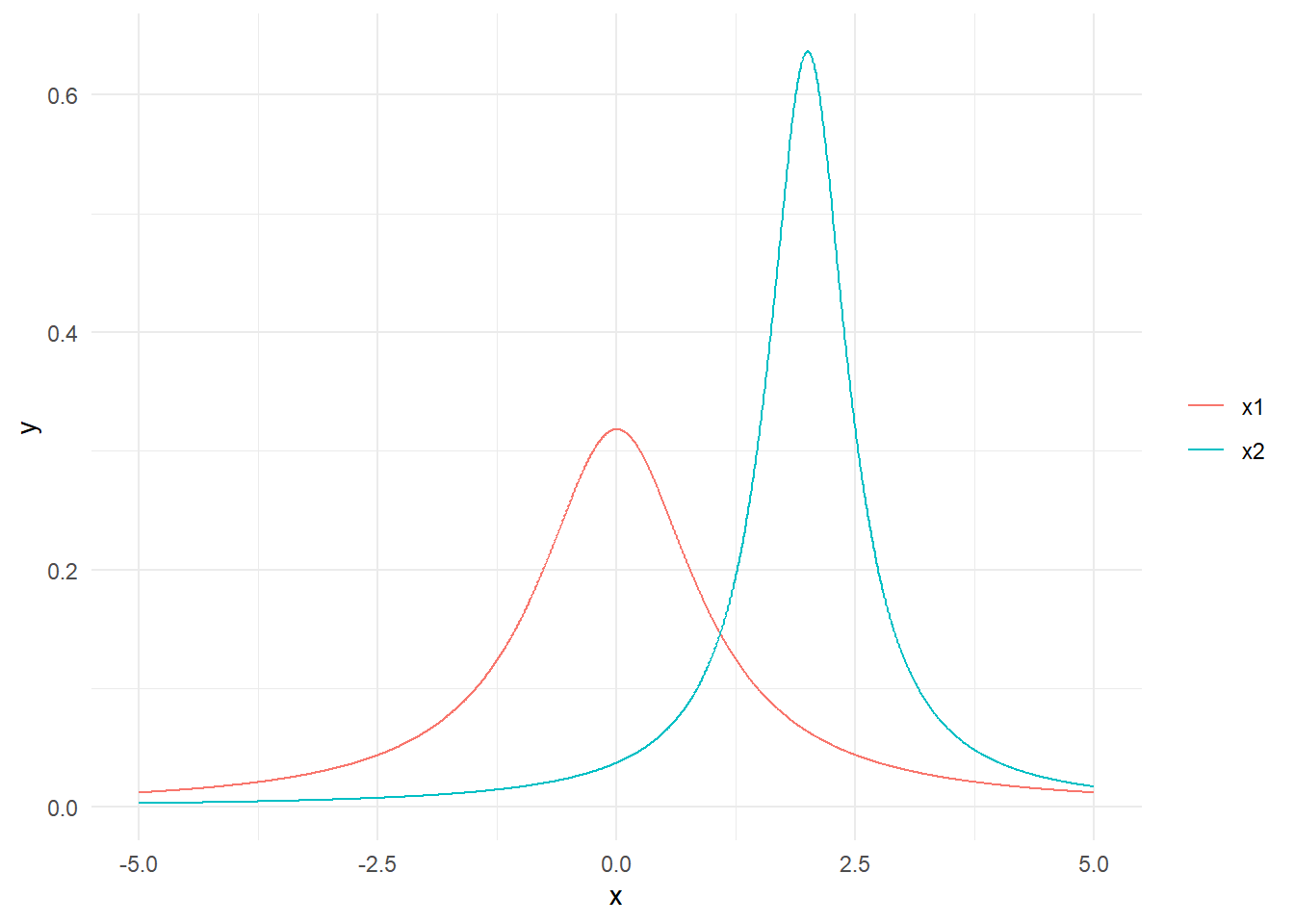
x1 <- rcauchy(n = n1, location = 0, scale = 1)
x2 <- rcauchy(n = n2, location = 2, scale = 0.5)
ggplot(data.frame(x = c(-5, 5)), aes(x)) +
stat_function(fun = dcauchy, n = 1500, args = list(location = 0, scale = 1), aes(color = "x1")) +
stat_function(fun = dcauchy, n = 1500, args = list(location = 2, scale = 0.5), aes(color = "x2")) +
theme_minimal() +
theme(legend.title = element_blank())x1、x2それぞれのサンプル内での群内順位を求めます。
rank_x1 <- rank(x1, ties.method = "average")
rank_x2 <- rank(x2, ties.method = "average")x1、x2を結合したサンプル内での順位(以降「全群内順位」)を求めます。
rank_x1_total <- rank(c(x1, x2), ties.method = "average") %>% head(n1)
rank_x2_total <- rank(c(x1, x2), ties.method = "average") %>% tail(n2)2群それぞれの平均群内順位を求めます。
rank_x1_avg <- (n1+1)/2
rank_x2_avg <- (n2+1)/22群それぞれの平均全群内順位を求めます。
Rank_x1_avg <- sum(rank_x1_total)/n1
Rank_x2_avg <- sum(rank_x2_total)/n22群それぞれの全群内順位と群内順位の差から不偏分散(\(S^2\))を求めます。
\[S^2=\dfrac{1}{n-1}\displaystyle\sum_{i=1}^n\left(\left(R_i-r_i\right)-\left(R-\dfrac{n+1}{2}\right)\right)^2 \tag{4}\]
S2_x1 <- 1/(n1-1)*sum((rank_x1_total-rank_x1 -(Rank_x1_avg-rank_x1_avg))^2)
S2_x2 <- 1/(n2-1)*sum((rank_x2_total-rank_x2 -(Rank_x2_avg-rank_x2_avg))^2)検定統計量(\(W\))を求めます.
\[W=\dfrac{n_1n_2(R_{x2}-R_{x1})}{(n_1+n_2)\sqrt{n_1S_{x1}^2+n_2S_{x2}^2}} \tag{5}\]
(W <- n1 * n2 * (Rank_x2_avg - Rank_x1_avg) / ((n1 + n2) * sqrt(n1 * S2_x1 + n2 * S2_x2)))[1] 5.874181自由度(\(f\))を求めます。
\[\hat{f} = \dfrac{\left(n_1 S_{x1}^2 + n_2 S_{x2}^2\right)^2}{\dfrac{\left(n_1 S_{x1}^2\right)^2}{n_1 - 1} + \dfrac{\left(n_2 S_{x2}^2\right)^2}{n_2 - 1}} \tag{6}\]
(f_hat <- (n1 * S2_x1 + n2 * S2_x2)^2 / ((n1 * S2_x1)^2 / (n1 - 1) + (n2 * S2_x2)^2 / (n2 - 1)))[1] 53.23587検定統計量\(W\)が自由度\(f\)のt分布に従うことを利用してp値(両側)を求めます。
pt(q = W, df = f_hat, lower.tail = F) * 2[1] 2.830664e-07「2つの群の母集団分布の確率論的等価性(stochastic equality)あるいは相対効果(relative effect)は同じ」との帰無仮説は有意水準5%で棄却されます。
brunnermunzel.test {brunnermunzel}を利用してBrunner-Munzel検定が行えます。
library(brunnermunzel)
brunnermunzel.test(x1, x2, "two.sided")
Brunner-Munzel Test
data: x1 and x2
Brunner-Munzel Test Statistic = 5.8742, df = 53.236, p-value =
2.831e-07
95 percent confidence interval:
0.7306926 0.9698788
sample estimates:
P(X<Y)+.5*P(X=Y)
0.8502857 以上です。