RでHPフィルター(Hodrick-Prescott filter)による時系列データの平滑化を試みます。
以下の資料を引用参照しています。
- https://www.imes.boj.or.jp/research/papers/japanese/kk17-6-2.pdf#page=10
- http://library.jsce.or.jp/jsce/open/00074/2008/52-07-0062.pdf
次の目的関数 Equation 1 を最小化する\(\tau\)を求めます。
\[\displaystyle\sum_{t=1}^n\left(y_t-\tau_t\right)^2+\lambda\displaystyle\sum_{t=3}^n\left[\left(\tau_t-\tau_{t-1}\right)-\left(\tau_{t-1}-\tau_{t-2}\right)\right]^2 \tag{1}\]
ここで、\(y_t\):時点tの観測値、\(\tau_t\): 時点tのトレンド成分、\(\lambda\):平滑化パラメータとし、Equation 1 を最小化するトレンド成分\(\tau\)を求めます。
なお、第一項はサイクル成分の2乗の総和、第二項はトレンド成分の2階差分の2乗の総和を意味します。
目的関数 Equation 1 を行列形式で表しますと、
\[\left(y-\tau\right)^{T}\left(y-\tau\right)+\lambda\left(\mathrm{D}_2\tau\right)^T\left(\mathrm{D}_2\tau\right) \tag{2}\]
ここで、\(y\):観測値のベクトル、\(\tau\):トレンド成分のベクトル、\(\mathrm{D}_2\):2階差分行列とし、\(\mathrm{D}_2\)は、
\[\left(\tau_t-\tau_{t-1}\right)-\left(\tau_{t-1}-\tau_{t-2}\right)=\tau_t-2\tau_{t-1}+\tau_{t-2}\] であることから、
\[\mathrm{D}_2=\begin{bmatrix} 1 & -2&1&0&\cdots&0 \\ 0 & 1&-2&1&\cdots&0\\ \vdots&\vdots&\vdots&\vdots&\ddots&\vdots\\ 0 & 0&\cdots&1&-2&1 \end{bmatrix}\]
目的関数 Equation 2 を\(\tau\)で微分し、0とおくことで、トレンド成分\(\tau\)の解が得られます。
\[\dfrac{\partial}{\partial_{\tau}}\left[\left(y-\tau\right)^{T}\left(y-\tau\right)+\lambda\left(\mathrm{D}_2\tau\right)^T\left(\mathrm{D}_2\tau\right)\right]=0 \tag{3}\]
整理しますと、
\[-2\left(y-\tau\right)+2\lambda\mathrm{D}_2^T\mathrm{D}_2\tau=0 \tag{4}\] と変形され、
\[ \begin{eqnarray} \tau&=&\left(I+\lambda\mathrm{D}_2^T\mathrm{D}_2\right)^{-1}y\\ &=&Sy \end{eqnarray} \tag{5}\] ここで、
\[S=\left(I+\lambda\mathrm{D}_2^T\mathrm{D}_2\right)^{-1}\] さらに、循環成分\(c\)は観測値\(y\)からトレンド成分\(\tau\)を減じることで求められます。
\[c=y-\tau \tag{6}\]
# サンプルデータの作成
library(dplyr)
library(ggplot2)
seed <- 20250223
set.seed(seed)
n <- 100
t <- seq(n)
trend <- seq(1, 10, length.out = n) + rnorm(n, 0, 0.5)
cycle <- sin(seq(0, 4 * pi, length.out = n)) + rnorm(n, 0, 0.2)
y <- trend + cycle
ggplot(mapping = aes(x = t, y = y)) +
geom_line() +
geom_point()# HPフィルターのパラメータ
lambda <- 1600
# HPフィルターの計算
I <- diag(n)
D2 <- matrix(0, n - 2, n)
for (i in 1:(n - 2)) {
D2[i, i:(i + 2)] <- c(1, -2, 1)
}
S <- solve(I + lambda * t(D2) %*% D2)
trend_hat <- S %*% y
cycle_hat <- y - trend_hat
# 結果のプロット
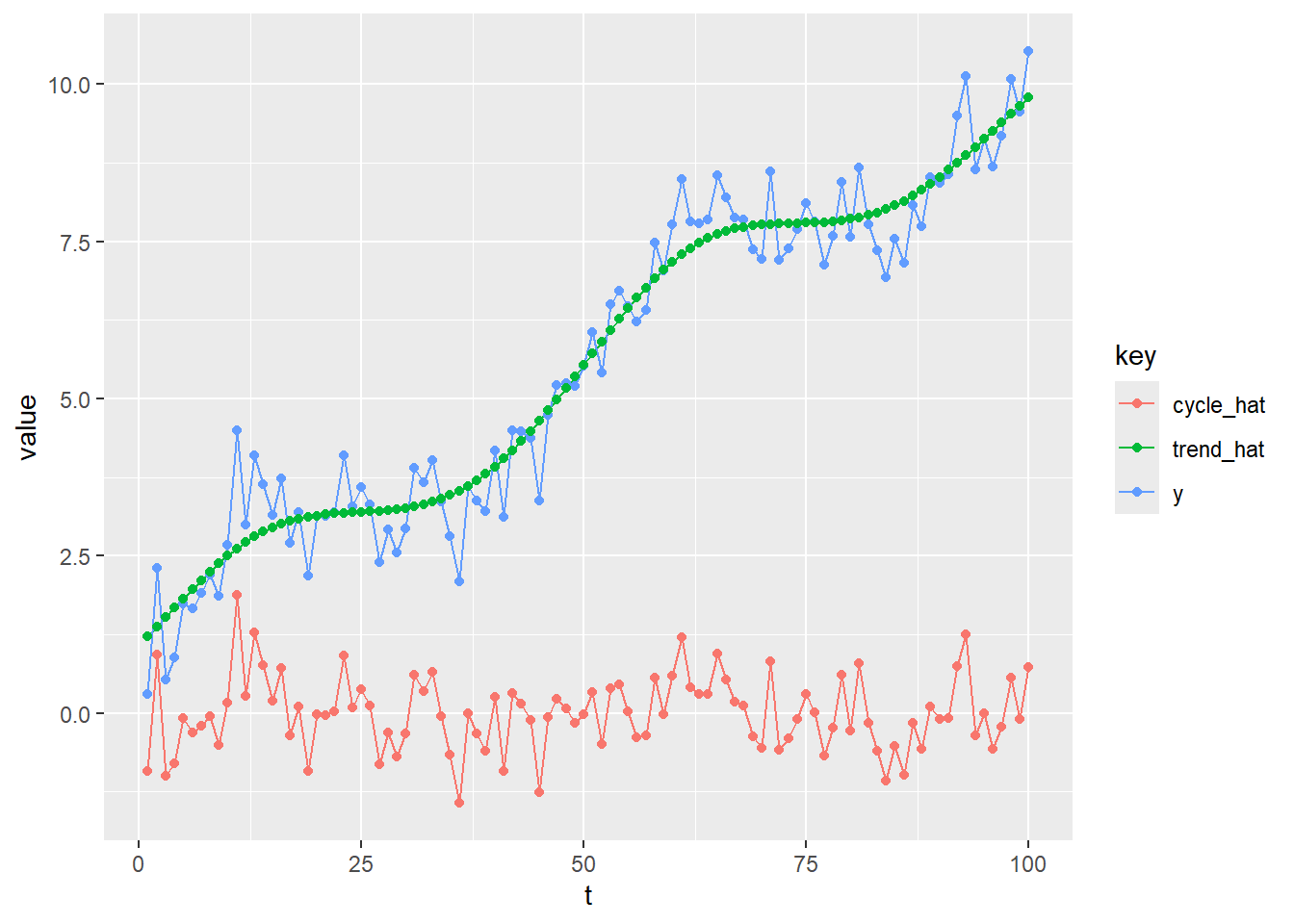
data.frame(t, y, trend_hat, cycle_hat) %>%
tidyr::gather(, , colnames(.)[-1]) %>%
ggplot(mapping = aes(x = t, y = value, colour = key)) +
geom_line() +
geom_point()Rの関数 hpfilter {mFilter} を利用してHPフィルターを掛けます。
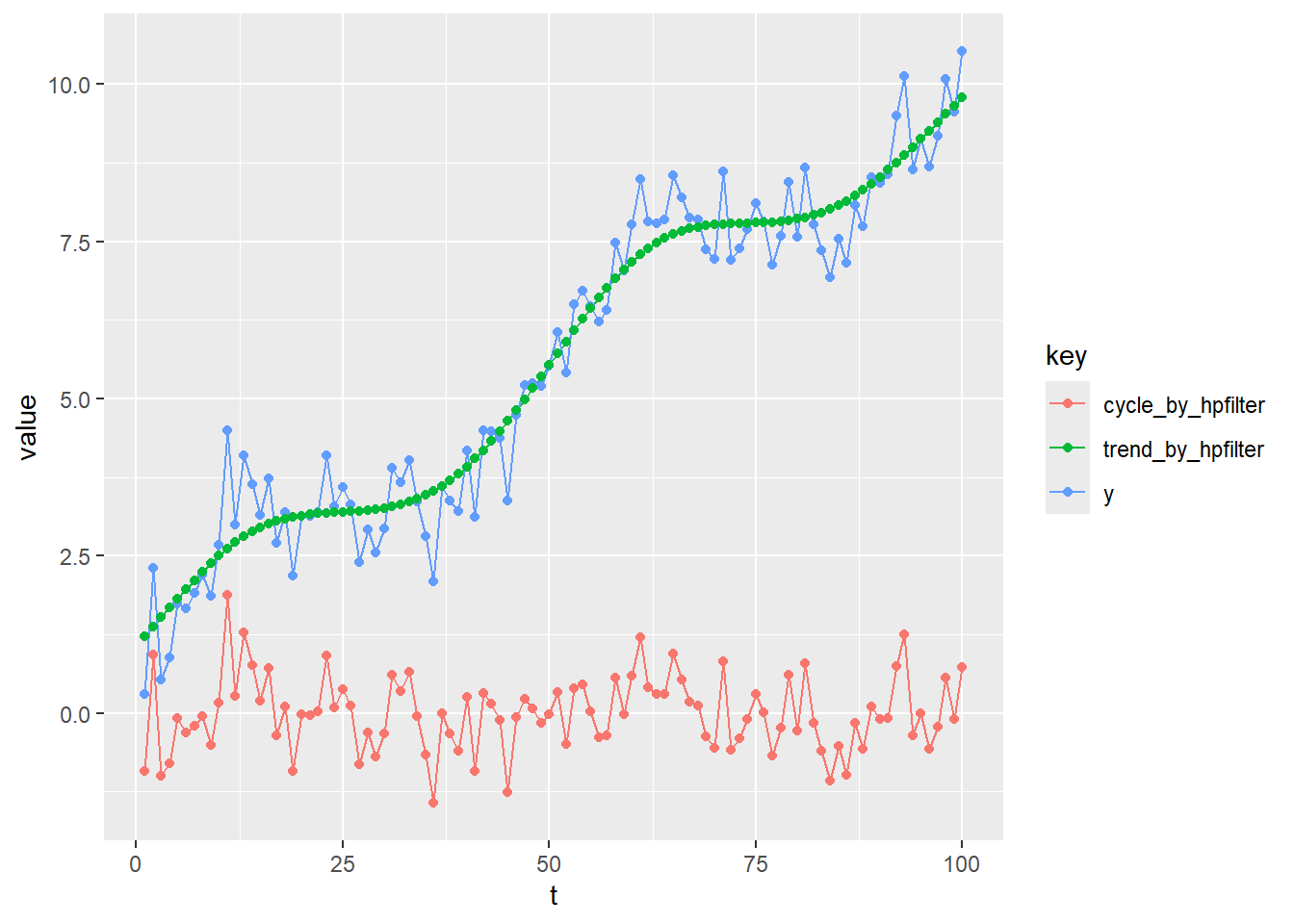
# HPフィルターの適用
hp_result <- mFilter::hpfilter(y, freq = lambda)
data.frame(t, y, trend_by_hpfilter = hp_result$trend, cycle_by_hpfilter = hp_result$cycle) %>%
tidyr::gather(, , colnames(.)[-1]) %>%
ggplot(mapping = aes(x = t, y = value, colour = key)) +
geom_line() +
geom_point()両者が一致していることを確認します。
unique(round(hp_result$trend - trend_hat, 11))
unique(round(hp_result$cycle - cycle_hat, 11)) [,1]
[1,] 0
[,1]
[1,] 0以上です。