Rを利用して分位点回帰を考えます。
以下の資料を引用参照しています。
- https://jasr.or.jp/wp/asr/asrpdf/asr14/asr14_070.pdf
- http://www.econ.uiuc.edu/~roger/research/rq/QRJEP.pdf
- http://www.econ.uiuc.edu/~roger/courses/Copenhagen/handouts/exercises.pdf
分位点回帰のメリットは大きく 2 つ,分布の裾の情報をみることで従来できなかった分析を可能にすること,分位点をみることで外れ値に対して頑健な分析を可能にすることが挙げられる。 出所:https://jasr.or.jp/wp/asr/asrpdf/asr14/asr14_070.pdf
誤差項が対称に分布して分散が均一なケースでは,古典的な回帰分析で得られる説明変数を与えたときの目的変数の平均的な動きや,後ほど紹介する最小絶対偏差回帰で得られる目的変数の条件付き中央値と,分位点回帰で得られる説明変数を与えたときの目的変数の分布の分位点との関係に違いはみられない。しかし,分散不均一のケースでは,条件付き分布の挙動は分位点ごとに異なっており,最小 2乗法で得られる条件付きの平均値だけでは,分布の挙動を正確に測ることができないことがわかる。 出所:https://jasr.or.jp/wp/asr/asrpdf/asr14/asr14_070.pdf
分位点が平均値と比べて極端に大きい値または小さい値である外れ値に対して頑健であり家計の所得・資産額などの社会・経済データの多くにみられる歪んだ分布をもつデータの分析に適していることが挙げられる。 出所:https://jasr.or.jp/wp/asr/asrpdf/asr14/asr14_070.pdf
分位点回帰は,条件付きの平均値ではなく条件付きの分位点を分析するものであるので,極端な値の影響を受けない頑健な分析を可能にするものと考えられる。 出所:https://jasr.or.jp/wp/asr/asrpdf/asr14/asr14_070.pdf
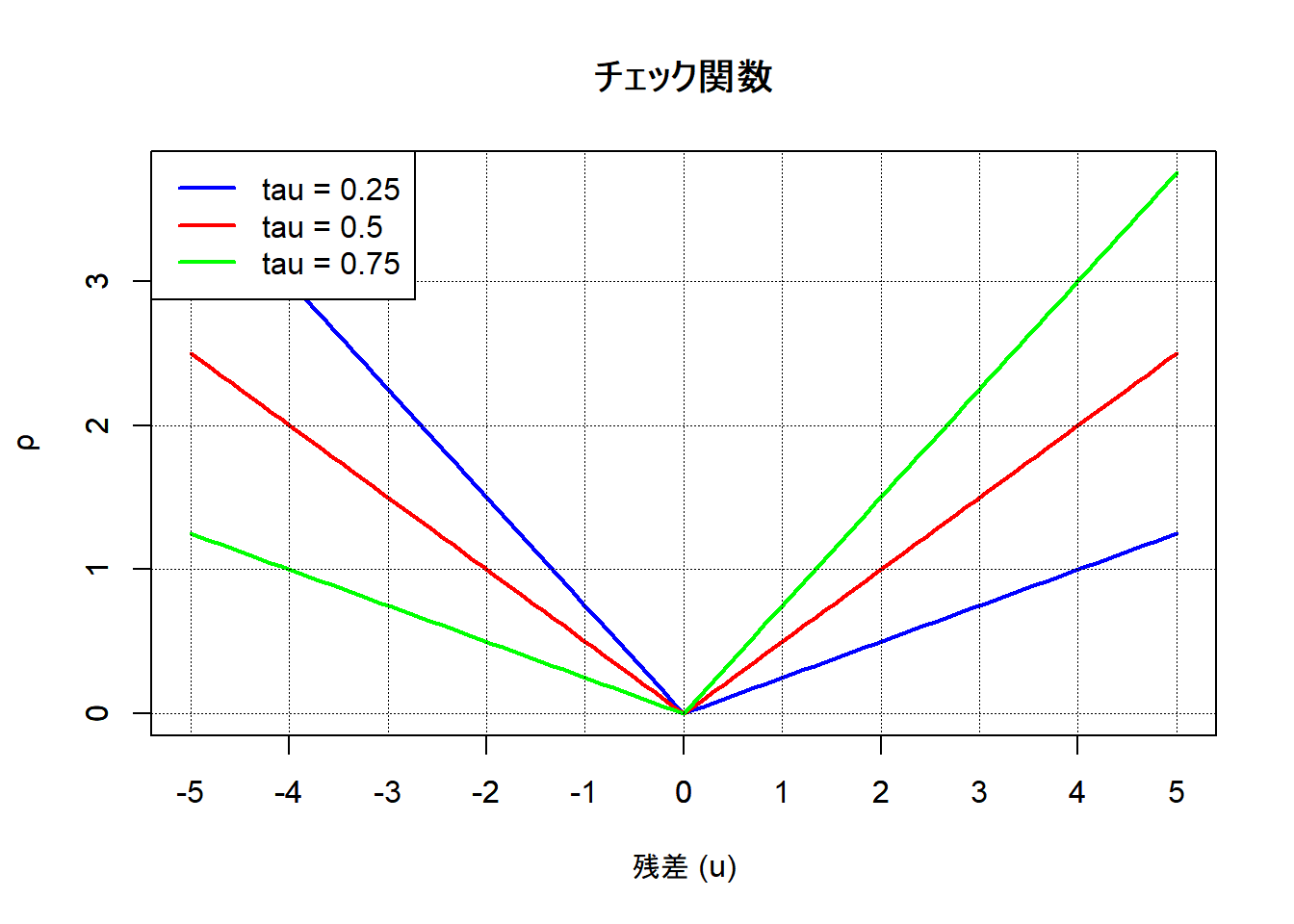
\[ \rho_{\tau}(u) = \begin{cases} (\tau - 1)\, u & \text{if } u \leq 0\\ \tau u & \text{if } u > 0 \end{cases} \] ここで、\(\rho_{\tau}(u)\) : チェック関数、\(\tau\) : 分位点\((0 < \tau < 1)\)、\(u\) : 残差 \((y - \hat{y})\) として、 \[\displaystyle\sum_{i=1}^n\rho_{\tau}\left(y_i-X_i^{'}\beta\right)\] を最小にする \(\beta\) を求めます。
チェック関数を確認します。
library(dplyr)
# チェック関数の定義
check_function <- function(u, tau) {
ifelse(u >= 0, tau * u, (tau - 1) * u)
}
# 残差の範囲
u <- c(seq(-5, 5, length.out = 99), 0) %>% sort()
# 分位点の設定
tau_values <- c(0.25, 0.5, 0.75)
# グラフの描画
plot(u, check_function(u, tau_values[1]),
type = "l",
xlab = "残差 (u)",
ylab = "ρ",
main = "チェック関数",
col = "blue",
lwd = 2
)
lines(u, check_function(u, tau_values[2]), col = "red", lwd = 2)
lines(u, check_function(u, tau_values[3]), col = "green", lwd = 2)
axis(side = 1, at = seq(-5, 5, 1), tck = 1.0, lty = "dotted", lwd = 0.5)
axis(side = 2, at = seq(0, 5, 1), tck = 1.0, lty = "dotted", lwd = 0.5)
# 凡例の追加
legend("topleft",
legend = paste("tau =", tau_values),
col = c("blue", "red", "green"),
lty = 1, lwd = 2
)始めにサンプルデータを作成します。
# サンプルデータの作成 (切片項を含む)
set.seed(20250208)
n <- 100
x <- runif(n)
y <- 1 + 2 * x + rnorm(n, sd = 0.5)続いて 分位点を \(\tau=0.5\) として分位点回帰を求めます。なお、最適化(最小値探索)には optim {stats} を利用します。
# 分位点の設定
tau <- 0.5 # 中央値回帰
# 目的関数 (チェック関数) の定義
check_function <- function(beta) {
residuals <- y - beta[1] - beta[2] * x # 切片項を考慮
sum(ifelse(residuals > 0, tau * residuals, (1 - tau) * abs(residuals)))
}
# 初期値の設定
initial_beta <- c(0, 0) # 切片と傾きの初期値を設定
# 最適化
result <- optim(initial_beta, check_function)
# 結果の表示
list("Intercept" = result$par[1], "Slope" = result$par[2])$Intercept
[1] 0.9857763
$Slope
[1] 1.87441線形回帰モデルによる結果との違いを確認します。
lm(y ~ x) %>% summary()
Call:
lm(formula = y ~ x)
Residuals:
Min 1Q Median 3Q Max
-1.0678 -0.4204 -0.1119 0.3919 1.8901
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.9792 0.1048 9.339 3.29e-15 ***
x 2.0957 0.2029 10.331 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.5615 on 98 degrees of freedom
Multiple R-squared: 0.5213, Adjusted R-squared: 0.5164
F-statistic: 106.7 on 1 and 98 DF, p-value: < 2.2e-16Rの関数 rq {quantreg} を利用して、分位点回帰による \(\beta\) を求めます。
library(quantreg)
# 分位点回帰の実行
rq(y ~ x, tau = tau)Call:
rq(formula = y ~ x, tau = tau)
Coefficients:
(Intercept) x
0.9858018 1.8743280
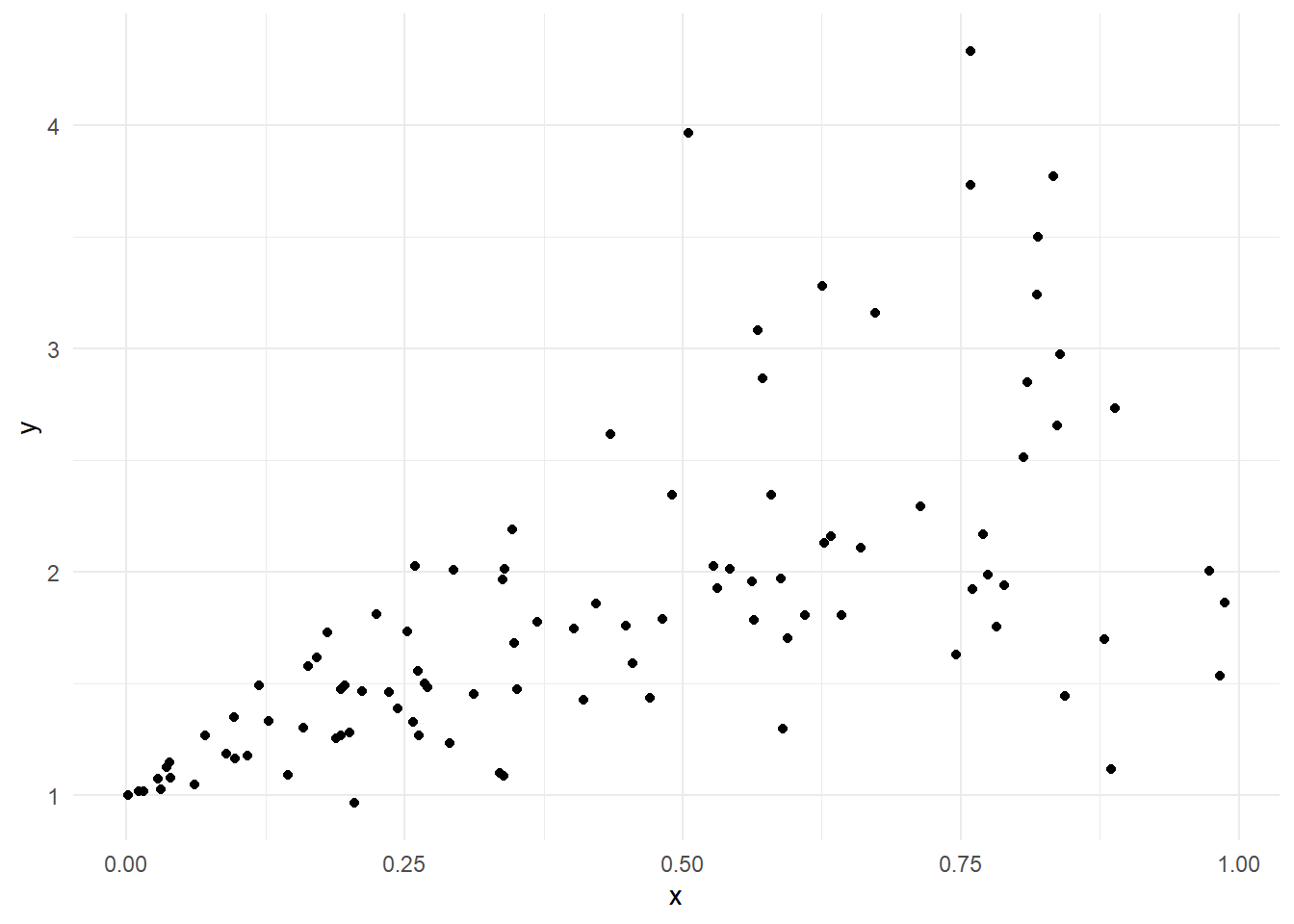
Degrees of freedom: 100 total; 98 residualもう一つサンプルデータを作成します。今回は残差の分散が不均一なサンプルとします。
library(ggplot2)
set.seed(20250208)
n <- 100
x <- runif(n) %>% sort()
y <- 1 + 2 * x + rnorm(n, sd = x)
(g <- ggplot(mapping = aes(x = x, y = y)) +
geom_point() +
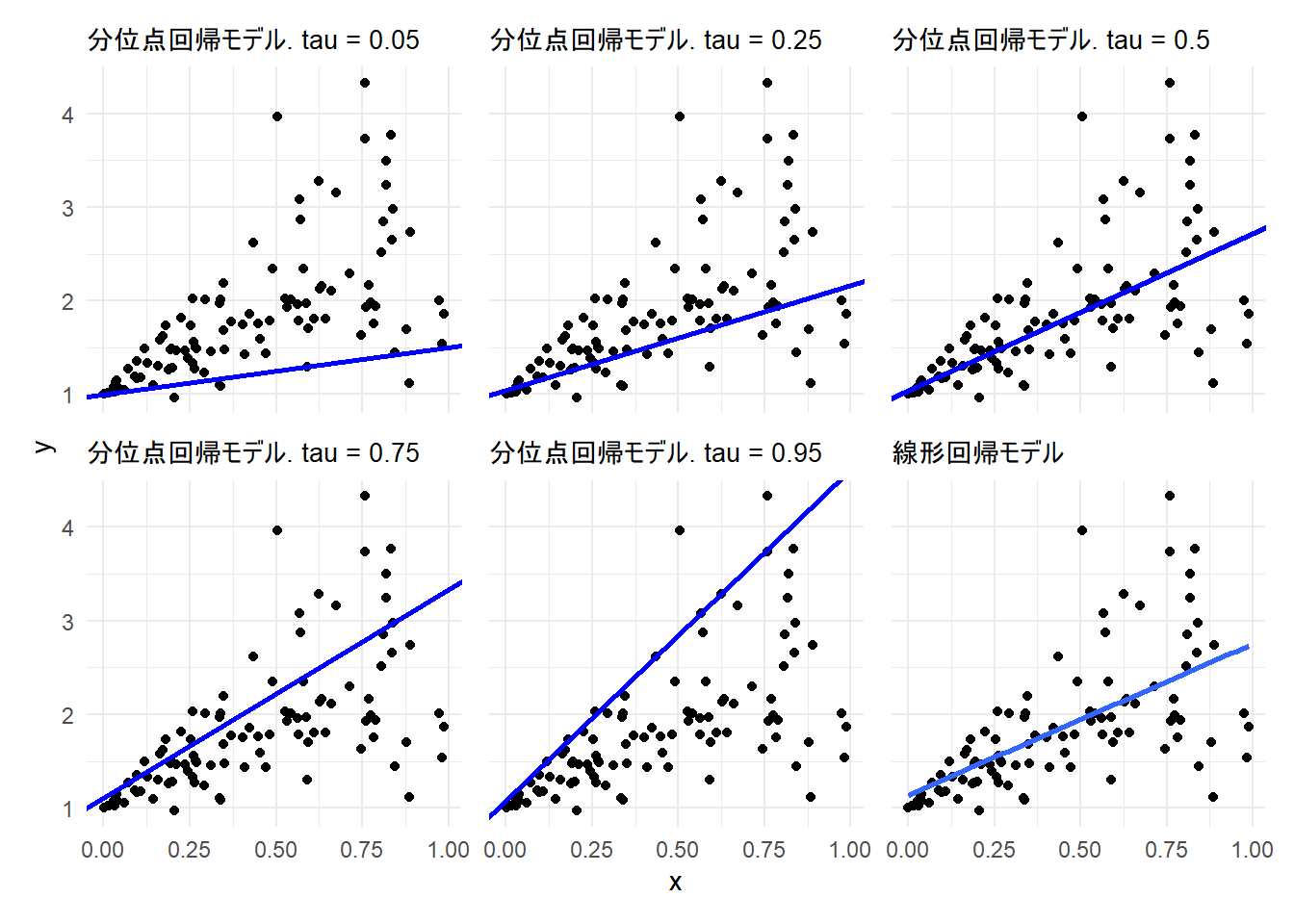
theme_minimal())分位点を5%、25%、50%、75%、95%とした回帰直線と線形回帰モデルの回帰直線とを比較します。
library(patchwork)
# 初期値の設定
initial_beta <- c(0, 0)
# 分位点回帰モデル
each_tau <- c(0.05, 0.25, 0.5, 0.75, 0.95)
gg <- list()
iii <- 1
for (iii in seq(each_tau)) {
tau <- each_tau[iii]
result <- optim(par = initial_beta, fn = check_function, method = "Nelder-Mead")
gg[[iii]] <- g + geom_abline(intercept = result$par[1], slope = result$par[2], color = "blue", linewidth = 1) + labs(title = paste0("分位点回帰モデル. tau = ", each_tau[iii])) + theme(plot.title = element_text(size = 10))
}
# 線形回帰モデル
gg[[iii + 1]] <- g + geom_smooth(method = "lm", se = F, linewidth = 1) + labs(title = "線形回帰モデル") + theme(plot.title = element_text(size = 10))
# 図の出力
Reduce(function(x, y) x + y, gg) +
plot_layout(axis_titles = "collect", axes = "collect")以上です。