時系列データを任意の時点で2つに分割した際に、分割前後の線形回帰の結果に有意な差があるか否かの検定です。
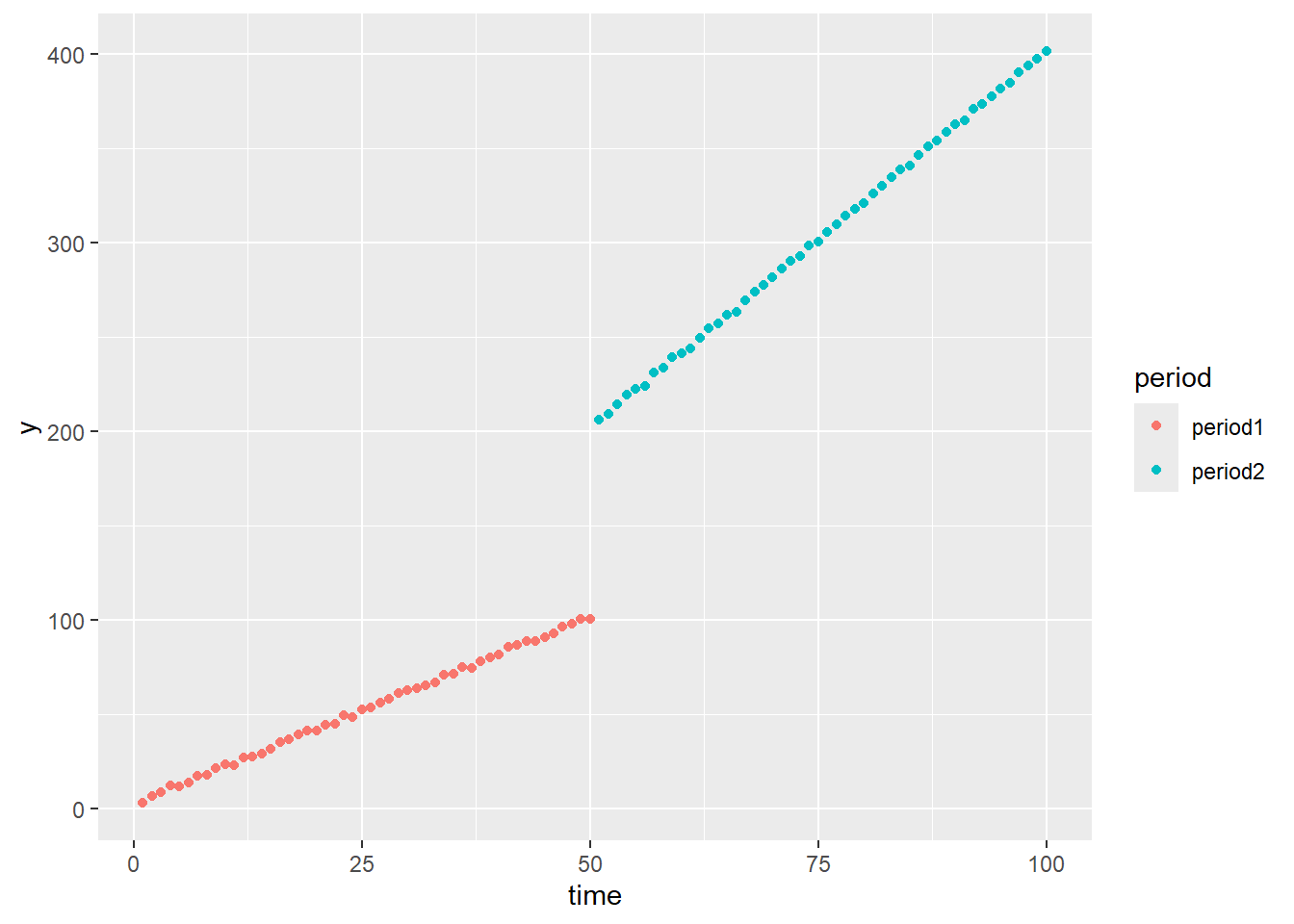
始めに切片は同一、傾きは異なるサンプルデータを作成します。サンプルサイズは100点とし、50点目で傾きのみ変化させます。
library(dplyr)
library(ggplot2)
fun_generate_sample <- function(seed, n, split_point, b0_period1, b0_period2, b1_period1, b1_period2) {
set.seed(seed)
time <- seq(n)
y <- numeric(length = n)
id_perion1 <- seq(n) %>% head(split_point)
id_perion2 <- seq(n) %>% tail(split_point)
y[id_perion1] <- b0_period1 + b1_period1 * time[seq(n) %>% head(split_point)] + rnorm(length(id_perion1))
y[id_perion2] <- b0_period2 + b1_period2 * time[seq(n) %>% tail(split_point)] + rnorm(length(id_perion2))
data <- data.frame(time = time, y = y)
data$period[id_perion1] <- "period1"
data$period[id_perion2] <- "period2"
data$period <- data$period %>% as.factor()
return(data)
}
data <- fun_generate_sample(seed = 20250315, n = 100, split_point = 50, b0_period1 = 2, b0_period2 = 2, b1_period1 = 2, b1_period2 = 4)
ggplot(data = data, mapping = aes(x = time, y = y, colour = period)) +
geom_point()period1 と period2 で傾きおよび切片に有意な差が生じているか検定します。有意水準は5%とします。
なお、説明変数 periodperiod2 は ピリオドの主効果(切片の差を捉える部分)であり、具体的には、基準ピリオド period1 からの切片の差を表します。
また、説明変数 time:periodperiod2 は時間とピリオドの交互作用効果(傾きの差を捉える部分)であり、具体的には、基準ピリオド period1 からの傾きの差を表します。
lm(y ~ time * period, data = data) %>% summary()
Call:
lm(formula = y ~ time * period, data = data)
Residuals:
Min 1Q Median 3Q Max
-2.53063 -0.61068 0.00182 0.74349 1.79597
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2.356380 0.264375 8.913 3.21e-14 ***
time 1.985696 0.009023 220.071 < 2e-16 ***
periodperiod2 -0.968878 0.742246 -1.305 0.195
time:periodperiod2 2.021544 0.012760 158.423 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.9207 on 96 degrees of freedom
Multiple R-squared: 1, Adjusted R-squared: 1
F-statistic: 7.009e+05 on 3 and 96 DF, p-value: < 2.2e-16結果のうち、
- (Intercept) は基準ピリオドである period1 の切片の推定値です。
- time は基準ピリオドである period1 の傾きの推定値です。
- periodperiod2 は period2 の切片が period1 の切片と比較してどれだけ異なるかを表す係数です。p値は0.195と95%信頼区間がゼロを跨ぎます。
- time:periodperiod2 は period2 の傾きが period1 の傾きと比較してどれだけ異なるかを表す係数です。p値は2e-16と95%信頼区間はゼロを跨ぎません。
periodperiod2 は棄却されず time:periodperiod2 棄却されますので、切片が同一との仮説は棄却されず、傾きは同一との仮説は棄却されます。
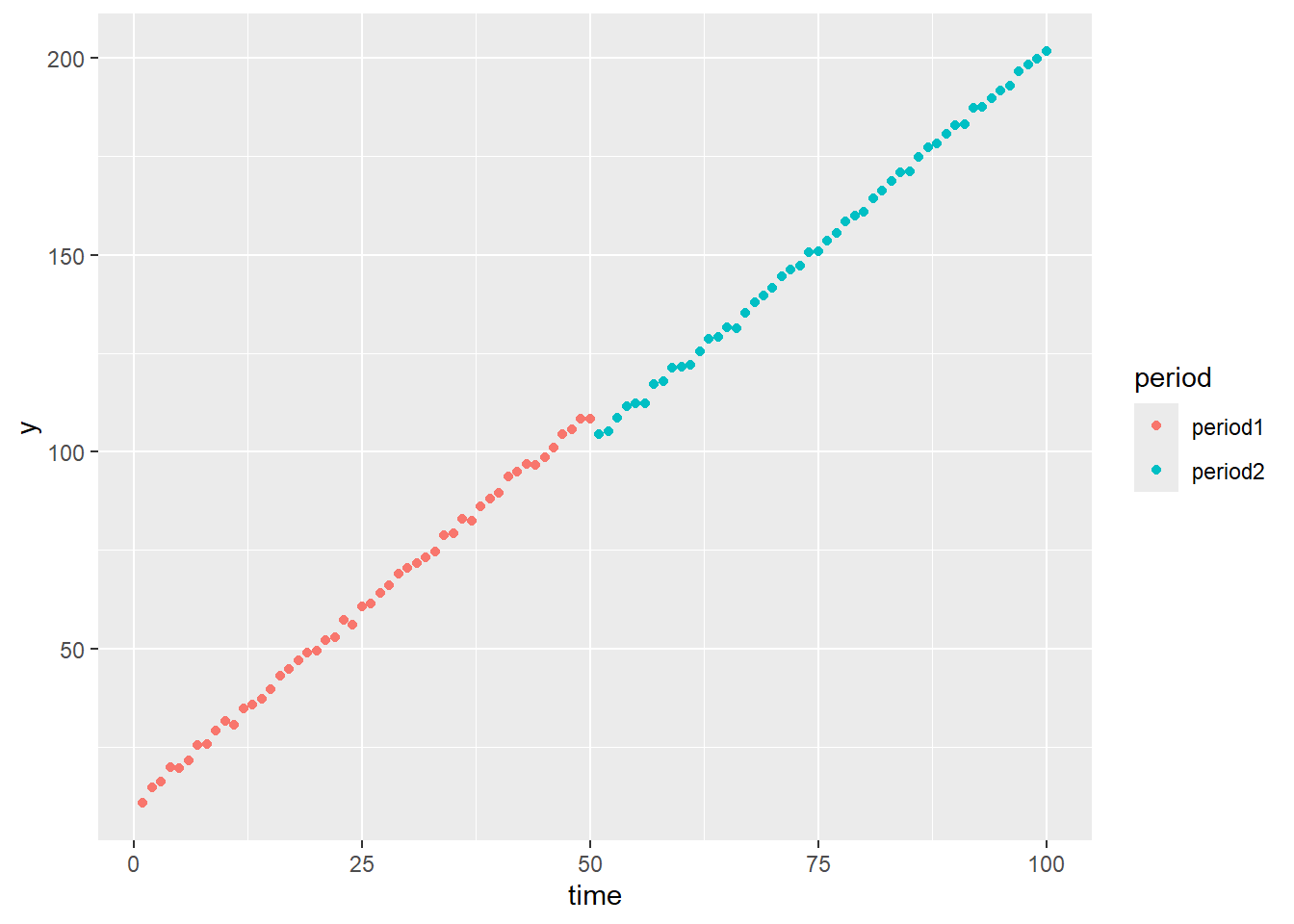
続いて傾きは同一、切片が異なるサンプルを確認します。
data <- fun_generate_sample(seed = 20250315, n = 100, split_point = 50, b0_period1 = 10, b0_period2 = 2, b1_period1 = 2, b1_period2 = 2)
ggplot(data = data, mapping = aes(x = time, y = y, colour = period)) +
geom_point()
lm(y ~ time * period, data = data) %>% summary()
Call:
lm(formula = y ~ time * period, data = data)
Residuals:
Min 1Q Median 3Q Max
-2.53063 -0.61068 0.00182 0.74349 1.79597
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 10.356380 0.264375 39.173 <2e-16 ***
time 1.985696 0.009023 220.071 <2e-16 ***
periodperiod2 -8.968878 0.742246 -12.083 <2e-16 ***
time:periodperiod2 0.021544 0.012760 1.688 0.0946 .
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.9207 on 96 degrees of freedom
Multiple R-squared: 0.9997, Adjusted R-squared: 0.9997
F-statistic: 1.157e+05 on 3 and 96 DF, p-value: < 2.2e-16切片は同一との仮説は棄却され、傾きは同一との仮説は棄却されません。
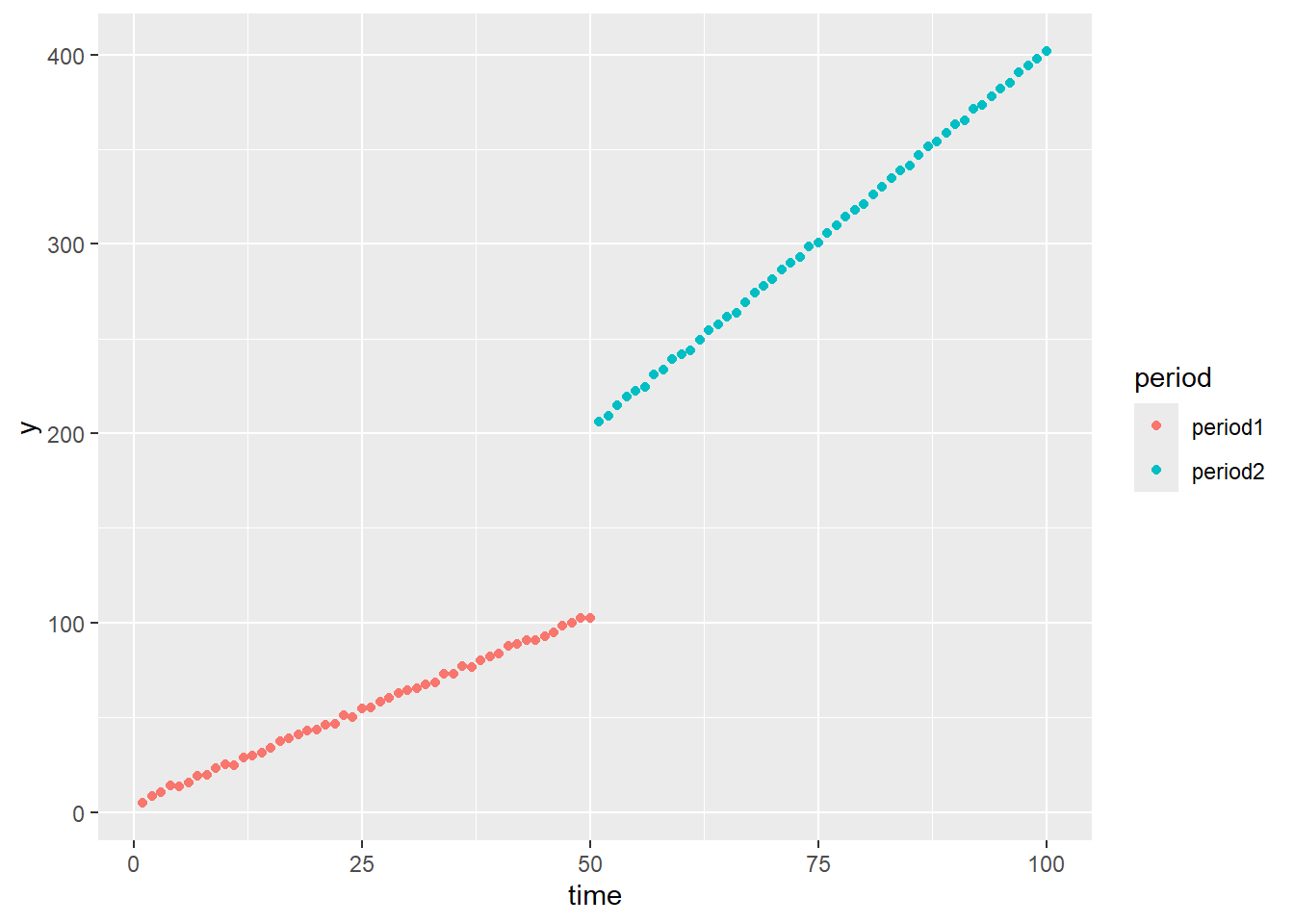
傾きも切片も異なるサンプルを確認します。
data <- fun_generate_sample(seed = 20250315, n = 100, split_point = 50, b0_period1 = 4, b0_period2 = 2, b1_period1 = 2, b1_period2 = 4)
ggplot(data = data, mapping = aes(x = time, y = y, colour = period)) +
geom_point()
lm(y ~ time * period, data = data) %>% summary()
Call:
lm(formula = y ~ time * period, data = data)
Residuals:
Min 1Q Median 3Q Max
-2.53063 -0.61068 0.00182 0.74349 1.79597
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 4.356380 0.264375 16.48 < 2e-16 ***
time 1.985696 0.009023 220.07 < 2e-16 ***
periodperiod2 -2.968878 0.742246 -4.00 0.000125 ***
time:periodperiod2 2.021544 0.012760 158.42 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.9207 on 96 degrees of freedom
Multiple R-squared: 1, Adjusted R-squared: 1
F-statistic: 6.911e+05 on 3 and 96 DF, p-value: < 2.2e-16切片、傾きとも両ピリオドで同一との仮説は棄却されます。
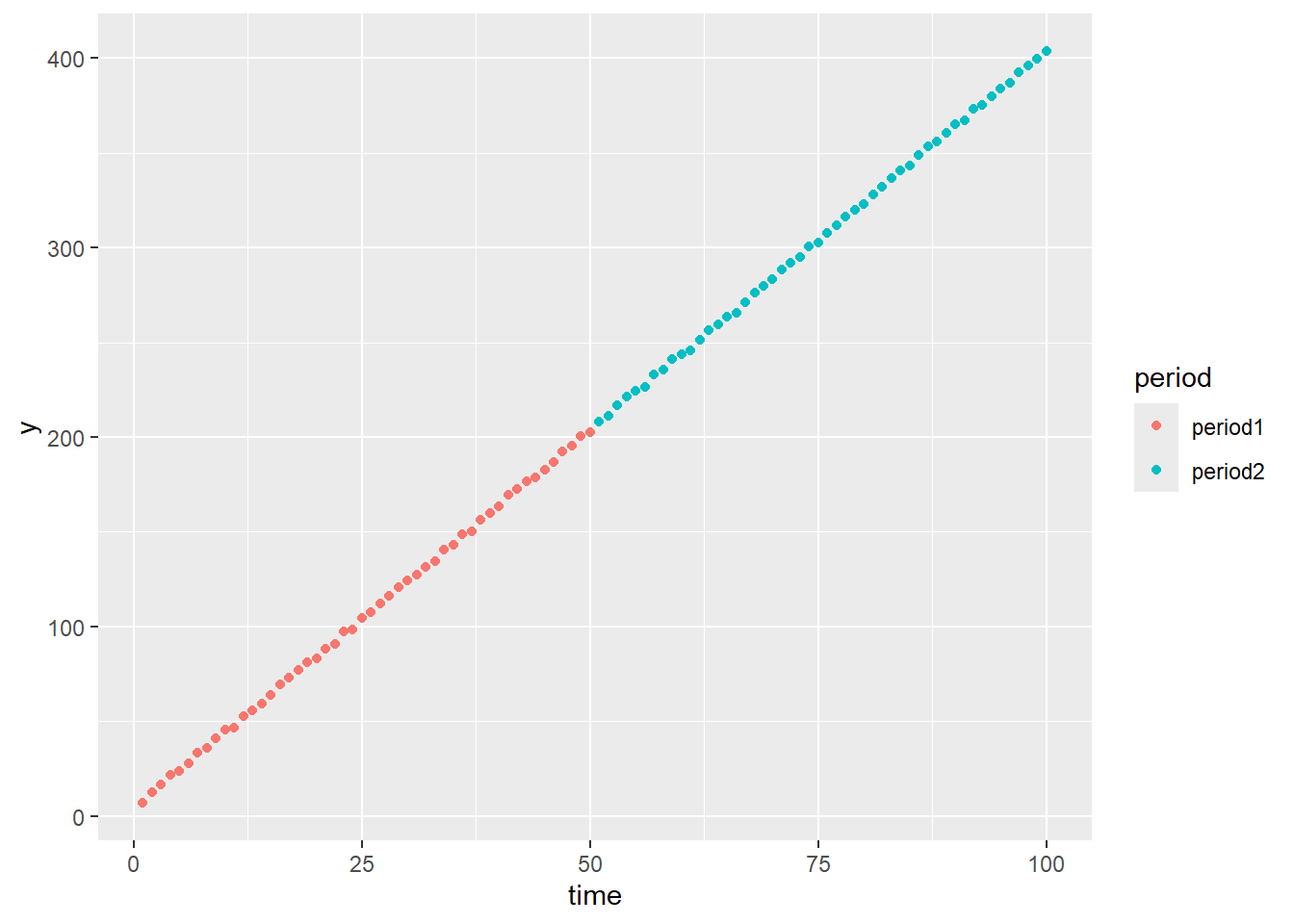
最後に傾きも切片も同一のサンプルで確認します。
data <- fun_generate_sample(seed = 20250315, n = 100, split_point = 50, b0_period1 = 4, b0_period2 = 4, b1_period1 = 4, b1_period2 = 4)
ggplot(data = data, mapping = aes(x = time, y = y, colour = period)) +
geom_point()
lm(y ~ time * period, data = data) %>% summary()
Call:
lm(formula = y ~ time * period, data = data)
Residuals:
Min 1Q Median 3Q Max
-2.53063 -0.61068 0.00182 0.74349 1.79597
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 4.356380 0.264375 16.478 <2e-16 ***
time 3.985696 0.009023 441.728 <2e-16 ***
periodperiod2 -0.968878 0.742246 -1.305 0.1949
time:periodperiod2 0.021544 0.012760 1.688 0.0946 .
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.9207 on 96 degrees of freedom
Multiple R-squared: 0.9999, Adjusted R-squared: 0.9999
F-statistic: 5.238e+05 on 3 and 96 DF, p-value: < 2.2e-16切片、傾きとも両ピリオドで同一との仮説は棄却されません。
以上です。