Rで 偏自己相関関数(Partial autocorrelation function) を試みます。
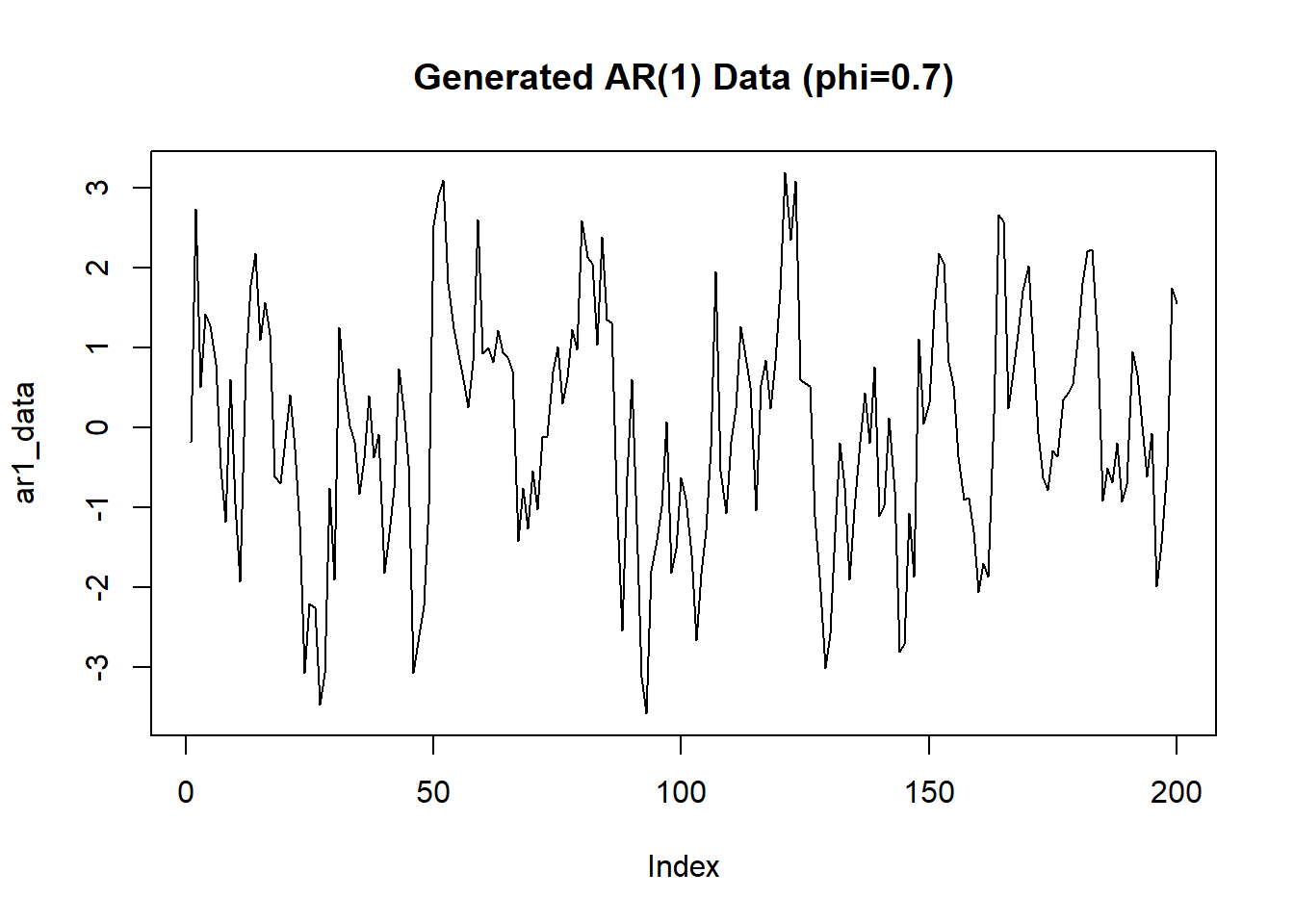
始めに AR(1) のサンプルデータを作成します。
seed <- 20250418
set.seed(seed)
n <- 200 # サンプルサイズ
phi1 <- 0.7 # AR(1)係数 |φ_1| < 1
noise_sd <- 1 # ノイズの標準偏差 σ_ε
# AR(1)プロセス: X_t = phi1 * X_{t-1} + epsilon_t
ar1_data <- numeric(n)
# 先頭のデータも定常分散から開始とする
# AR(1) プロセス(平均 0 と仮定)の分散 Var(X_t) は、時間(t)によらず一定の値 γ(0) をとる
# Var(X_t) = Var(φ_1 * X_{t-1} + ε_t) = φ_1^2 * Var(X_{t-1}) + Var(ε_t)
# ノイズ ε_t の分散を σ²_ε とする
# γ(0) = φ_1^2 * γ(0) + σ²_ε
# γ(0) - φ_1^2 * γ(0) = σ²_ε
# γ(0) * (1 - φ_1^2) = σ²_ε
# γ(0) = σ²_ε / (1 - φ_1^2)
# SD(X_t) = sqrt(γ(0)) = σ_ε / sqrt(1 - φ_1^2)
ar1_data[1] <- rnorm(1, mean = 0, sd = noise_sd / sqrt(1 - phi1^2))
for (t in 2:n) {
ar1_data[t] <- phi1 * ar1_data[t - 1] + rnorm(1, mean = 0, sd = noise_sd)
}
plot(ar1_data, type = "l", main = "Generated AR(1) Data (phi=0.7)")自己相関関数(ACF) を求める関数。
calculate_acf <- function(x, max_lag) {
n <- length(x)
x_mean <- mean(x)
x_centered <- x - x_mean
# 分散 (gamma(0)) の計算
gamma0 <- sum(x_centered^2) / n
acf_values <- numeric(max_lag + 1)
acf_values[1] <- 1.0 # ACF(0) は常に 1
# ラグ 1 から max_lag までのACFを計算
for (h in 1:max_lag) {
# 自己共分散 gamma(h) の計算
gamma_h <- sum(x_centered[(h + 1):n] * x_centered[1:(n - h)]) / n
acf_values[h + 1] <- gamma_h / gamma0 # ACF(h) = gamma(h) / gamma(0)
}
# ラグ0からmax_lagまでの値を返す (長さ max_lag + 1)
return(acf_values)
}偏自己相関関数(PACF) を求める関数。
calculate_pacf <- function(x, max_lag) {
n <- length(x)
# 始めに、必要なラグまでのACFを計算
# ACFはラグ0からmax_lagまで必要 (長さは max_lag + 1)
acf_vals <- calculate_acf(x, max_lag)
pacf_vals <- numeric(max_lag) # 結果を格納するベクトル (ラグ1からmax_lagまで)
# --- ラグ 1 の PACF ---
# PACF(1) = ACF(1)
pacf_vals[1] <- acf_vals[2] # acf_valsのインデックス2がラグ1に対応
# --- ラグ 2 から max_lag までの PACF ---
if (max_lag >= 2) {
for (k in 2:max_lag) {
# Yule-Walker方程式を解くための準備
# Γ_k * φ_k = γ_k
# 自己相関行列 Γ_k (k x k) を構築
# Γ_k[i, j] = ρ(|i-j|) = acf_vals[abs(i - j) + 1]
Gamma_k <- matrix(0, nrow = k, ncol = k)
for (i in 1:k) {
for (j in 1:k) {
lag_index <- abs(i - j) + 1
Gamma_k[i, j] <- acf_vals[lag_index]
}
}
# 自己相関ベクトル γ_k (k x 1) を構築
# γ_k = [ρ(1), ρ(2), ..., ρ(k)]^T = acf_vals[2:(k+1)]
gamma_k_vec <- acf_vals[2:(k + 1)]
# Γ_k * φ_k = γ_k を解いて φ_k を求める
# solve(A, b) は Ax = b の x を返す
phi_k_solution <- solve(Gamma_k, gamma_k_vec)
# PACF(k) は解 φ_k の最後の要素 φ_kk
pacf_vals[k] <- phi_k_solution[k]
}
}
# ラグ1からmax_lagまでの値を返す (長さ max_lag)
names(pacf_vals) <- 1:max_lag # 結果にラグ番号の名前をつける
return(pacf_vals)
}サンプルデータの 偏自己相関関数 を求めます。
max_lag_to_calculate <- 20 # 計算する最大ラグ
# PACFを計算
(pacf_results <- calculate_pacf(ar1_data, max_lag_to_calculate)) 1 2 3 4 5 6
0.69237188 -0.11174151 -0.05143607 0.02472952 -0.01515109 -0.07934668
7 8 9 10 11 12
-0.05351803 -0.11372046 0.09839197 0.04321378 -0.03823214 -0.02222230
13 14 15 16 17 18
-0.03082981 0.02400196 0.03427041 0.06812720 -0.20009914 -0.01829678
19 20
0.02378457 -0.08653871 95%信頼区間を求めます。
confidence_level <- 0.95
alpha <- 1 - confidence_level
# Zスコアを計算
z_score <- qnorm(1 - alpha / 2)
# 信頼区間の上限と下限を計算
(conf_limit_upper <- z_score / sqrt(n))
(conf_limit_lower <- -z_score / sqrt(n))[1] 0.1385904
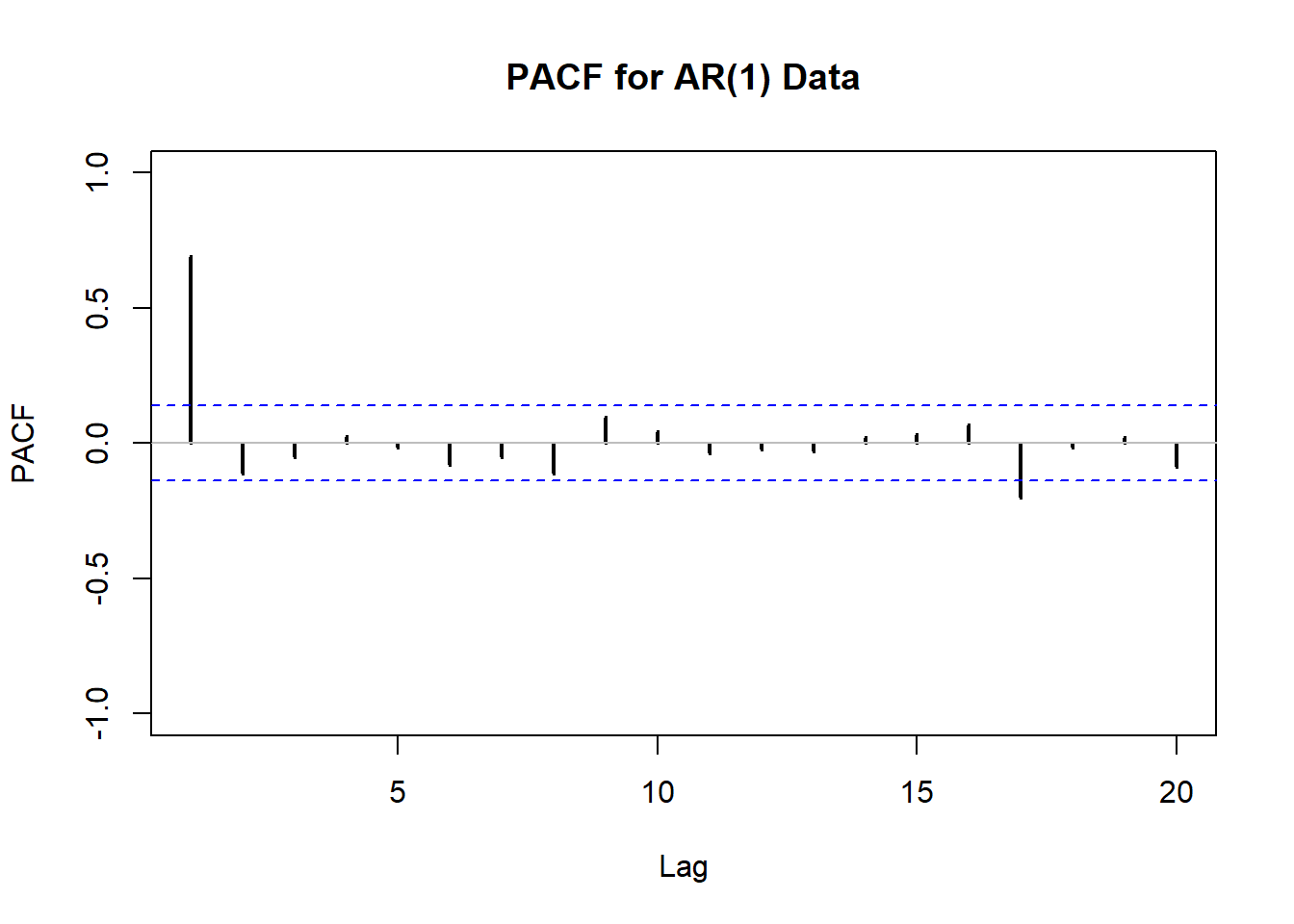
[1] -0.1385904結果を可視化します。
plot(1:max_lag_to_calculate, pacf_results,
type = "h", lwd = 2,
ylim = c(-1, 1), xlab = "Lag", ylab = "PACF",
main = "PACF for AR(1) Data"
)
abline(h = 0, col = "gray")
abline(h = c(conf_limit_upper, -conf_limit_upper), lty = 2, col = "blue")Rの関数 pacf {stats} と比較します。
(pacf_builtin <- pacf(ar1_data, lag.max = max_lag_to_calculate, plot = FALSE))
Partial autocorrelations of series 'ar1_data', by lag
1 2 3 4 5 6 7 8 9 10 11
0.692 -0.112 -0.051 0.025 -0.015 -0.079 -0.054 -0.114 0.098 0.043 -0.038
12 13 14 15 16 17 18 19 20
-0.022 -0.031 0.024 0.034 0.068 -0.200 -0.018 0.024 -0.087 unique(round(as.vector(pacf_builtin$acf) - pacf_results, 14))[1] 0一致しています。
以上です。