Rで 誤差構造 を ガンマ分布、リンク関数 を log とする 一般化線形モデル を試みます。
始めにサンプルデータを作成します。
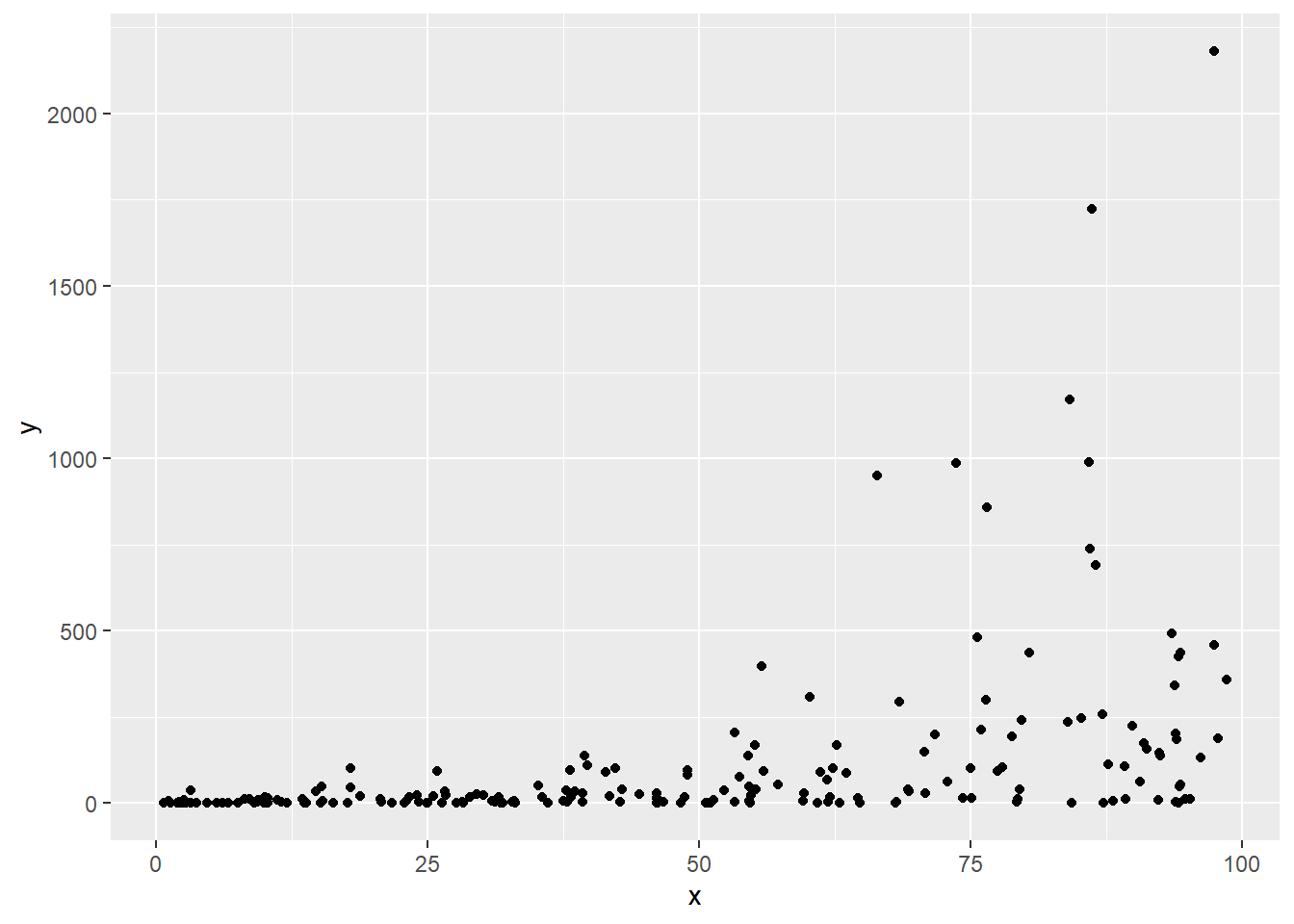
サンプルデータは 0-100 の範囲を取る説明変数と、ガンマ分布 に従う従属変数の組み合わせとします。
library(ggplot2)
seed <- 20250406
set.seed(seed)
n_obs <- 200 # サンプルサイズ
# 説明変数 X (0から100の範囲とします)
x <- runif(n_obs, 0, 100)
# 真のパラメータを設定
beta_true <- c(1.5, 0.05) # 真の切片 (beta0) と傾き (beta1) (logスケール)
phi_true <- 2.0 # 真の分散パラメータ (dispersion parameter)
# phiが大きいほど分散が大きい (Var = phi * mu^2)
# デザイン行列を作成 (切片項を含む)
X <- cbind(1, x)
# 線形予測子 eta = X * beta (logスケール)
eta_true <- X %*% beta_true
# 平均 mu を計算 (逆対数リンク関数 = 指数関数)
mu_true <- exp(eta_true)
# 従属変数 y を生成 (ガンマ分布に従う)
# Rのrgamma(n, shape, rate)を使う。
# glmのGammaファミリー(link="log")の定義 Var(Y) = phi * E[Y]^2 = phi * mu^2 に合わせる。
# ガンマ分布の性質 E[Y] = shape/rate, Var(Y) = shape/rate^2
# shape/rate = mu
# shape/rate^2 = phi * mu^2
# これらを解くと、shape = 1/phi, rate = 1/(phi * mu)
shape_param <- 1 / phi_true
rate_param <- 1 / (phi_true * mu_true)
y <- rgamma(n_obs, shape = shape_param, rate = rate_param)
# 可視化します
ggplot(mapping = aes(x = x, y = y)) +
geom_point()続いて、Iteratively Reweighted Least Squares (IRLS) アルゴリズム を用いてパラメータ(回帰係数 \(\beta\))を推定します。
# 初期値設定
# 対数変換したyでOLS推定した値を初期値にする
(beta_current <- lm.fit(X, log(pmax(y, 1e-6)))$coefficients)
max_iter <- 50 # 最大反復回数
tolerance <- 1e-7 # 収束判定の閾値
epsilon <- 1e-9 # μの下限値
for (iter in 1:max_iter) {
# (1) 線形予測子 η (eta) の計算
eta <- X %*% beta_current
# (2) 平均 μ (mu) の計算 (逆対数リンク関数 = 指数関数)
mu <- exp(eta)
# mu が非常に小さくならないように調整
mu <- pmax(mu, epsilon)
# (3) 従属変数(一時的) z の計算
# z = η + (y - μ) * g'(μ) = η + (y - μ) / μ
z <- eta + (y - mu) / mu
# (4) β の更新
beta_new <- solve(t(X) %*% X) %*% t(X) %*% z
# (5) 収束判定
delta <- sum((beta_new - beta_current)^2)
print(paste("Iteration:", iter, " Change in Beta:", round(delta, 8)))
beta_current <- beta_new
if (delta < tolerance) {
print(paste("収束しました (反復回数:", iter, ")"))
break
}
if (iter == max_iter) {
warning("最大反復回数に達しました。収束していない可能性があります。")
}
}
beta_estimated <- beta_current x
-0.10411157 0.05273673
[1] "Iteration: 1 Change in Beta: 17.67563325"
[1] "Iteration: 2 Change in Beta: 0.87275387"
[1] "Iteration: 3 Change in Beta: 0.66959384"
[1] "Iteration: 4 Change in Beta: 0.30429974"
[1] "Iteration: 5 Change in Beta: 0.03918633"
[1] "Iteration: 6 Change in Beta: 0.00060953"
[1] "Iteration: 7 Change in Beta: 2e-06"
[1] "Iteration: 8 Change in Beta: 1e-08"
[1] "収束しました (反復回数: 8 )"推定された回帰係数 \(\beta\) です。
beta_estimated [,1]
1.57185851
x 0.04811505分散パラメータ \(\phi\) (Dispersion parameter) を推定します。
# 推定された β を使って最終的な μ を計算
eta_final <- X %*% beta_estimated
mu_final <- exp(eta_final)
mu_final <- pmax(mu_final, epsilon)
# ピアソン残差を計算
# ガンマ分布の分散関数 V(μ) = μ^2 なので、
# ピアソン残差 r_p = (y - μ) / sqrt(V(μ)) = (y - μ) / μ
pearson_residuals <- (y - mu_final) / mu_final
# ピアソンカイ二乗統計量を計算
pearson_chi2 <- sum(pearson_residuals^2)
# φ のモーメント推定量 (ピアソンカイ二乗統計量を自由度で割る)
p <- ncol(X) # 推定した回帰係数の数
(phi_estimated <- pearson_chi2 / (n_obs - p))[1] 2.233302Rの関数 glm の結果と比較します。
fit_glm_gamma <- glm(y ~ x, family = Gamma(link = "log"))
summary(fit_glm_gamma)
Call:
glm(formula = y ~ x, family = Gamma(link = "log"))
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.571859 0.203104 7.739 5.01e-13 ***
x 0.048115 0.003562 13.510 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for Gamma family taken to be 2.233302)
Null deviance: 906.51 on 199 degrees of freedom
Residual deviance: 580.36 on 198 degrees of freedom
AIC: 1856.7
Number of Fisher Scoring iterations: 9beta_estimated と一致しています。
glm の結果と比較します。
eta_pred <- X %*% beta_estimated
mu_pred <- exp(eta_pred)
mu_pred_glm <- predict(fit_glm_gamma, newdata = data.frame(x = x), type = "response")
unique(round(mu_pred - mu_pred_glm, 10)) [,1]
[1,] 0一致しています。
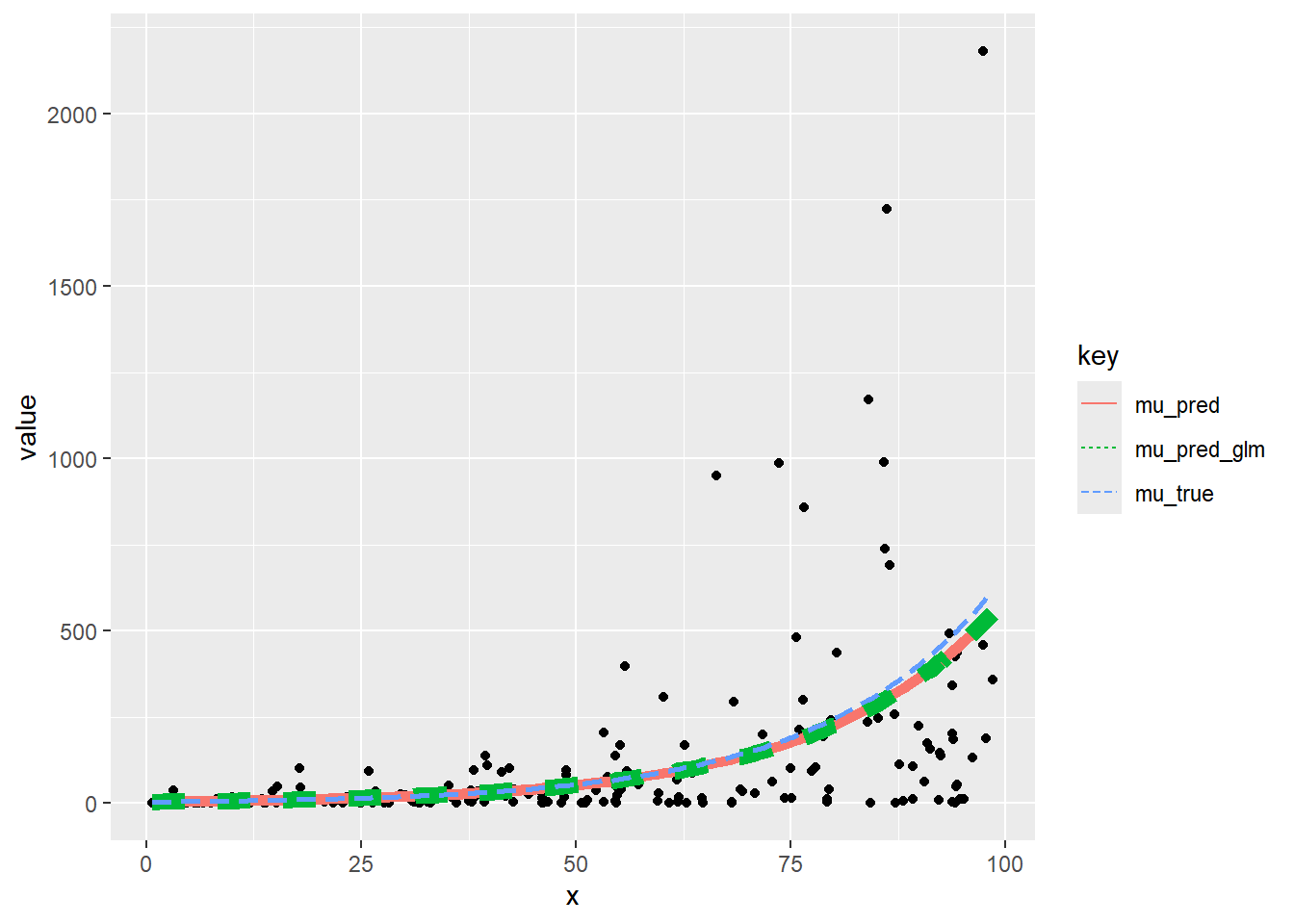
図で確認します。
library(dplyr)
# 真の関係 (平均μ)
eta_pred_true <- X %*% beta_true
mu_true <- exp(eta_pred_true)
tidydf <- data.frame(x, y, mu_true, mu_pred, mu_pred_glm) %>% tidyr::gather(, , colnames(.)[-1])
ggplot(data = tidydf, mapping = aes(x = x, y = value, colour = key)) +
geom_point(data = subset(tidydf, key == "y"), colour = "black") +
geom_line(
data = subset(tidydf, key %in% c("mu_true", "mu_pred", "mu_pred_glm")),
mapping = aes(
group = key,
linetype = key,
linewidth = ifelse(key == "mu_true", 1, ifelse(key == "mu_pred", 2, 3))
)
) +
scale_linewidth_identity(
breaks = c(1, 2, 3),
labels = c("mu_true", "mu_pred", "mu_pred_glm")
)以上です。