Rによる 自己相関関数 の 臨界値(Critical Value) 算出を試みます。
本ポストは http://feldman.faculty.pstat.ucsb.edu/174-03/lectures/l12.pdf を参照しています。
自己相関関数の臨界値の目的は、あるラグ \(h(>0)\) における 真の自己相関 \(\rho_h\) についての以下の検定です。
\(\mathrm{H_0}:\rho_h=0\) (自己相関なし=ホワイトノイズ)、\(\mathrm{H_1}:\rho_h\neq0\) (自己相関あり)
時系列データ \(x_t,\,\small{t=(1,\cdots,n)}\)における、ラグ \(h\) の 標本自己相関 \(r_h\) の定義は、
\[
r_h = \dfrac{\displaystyle\sum_{t=1}^{n - h} \left(x_t - \bar{x}\right)\left(x_{t + h} - \bar{x}\right)}{\displaystyle\sum_{t=1}^{n} \left(x_t - \bar{x}\right)^2}
\] ここで、\(\bar{x}\) は時系列 \(x_t\) の標本平均 \(\bar{x} = \dfrac{1}{n} \displaystyle\sum_{t=1}^{n} x_t\)、分子はラグ \(h\) における 標本自己共分散、分母は 標本分散 です。
よって、標本自己共分散を \(c_h\)、標本分散 \(c_0\) としますと、標本自己相関 \(r_h\) は
\[r_h=\dfrac{c_h}{c_0}\] 以降、仮説検定のため、\(x_t\) を ホワイトノイズ かつ 大標本(\(n\rightarrow\infty\))と仮定します。
- 独立かつ同一分布(i.i.d.) : 各 \(x_t\) は互いに独立で、同じ分布に従う。
- 期待値 : \(E\left[x_t\right]=0\)
- 分散 : \(\mathrm{Var}\left(x_t\right)=\sigma^2\)
- 共分散 : \(\mathrm{Cov}\left(x_t, x_{t + h}\right) = 0\) (\(h > 0\) のとき)
始めに上記仮定のもとで、ラグ \(h\) における標本自己相関の標準誤差が \(\dfrac{1}{\sqrt{n}}\) に近似されることを導出します。
\(h>0\) において \(c_h\) の期待値は、\(x_t\) と \(x_{t+h}\) が独立であるため、 \[\mathrm{E}\left[c_h\right]=0\]
\(c_h\) の分散を求めますと
\[\mathrm{Var}(c_h)=\mathrm{E}\left[c_h^2\right]-\left(\mathrm{E}\left[c_h\right]\right)^2=\mathrm{E}\left[c_h^2\right]\] 展開しますと、
\[
\begin{eqnarray}
c_h^2&=&\left(\dfrac{1}{n}\displaystyle\sum_{t=1}^{n-h}\left(x_t-0\right)\left(x_{t+h}-0\right)\right)^2=\dfrac{1}{n^2}\displaystyle\sum_{t=1}^{n-h}\displaystyle\sum_{s=1}^{n-h}x_t\cdot x_{t+h}\cdot x_s\cdot x_{s+h}\\
\mathrm{E}\left[c_h^2\right]&=&\dfrac{1}{n^2}\mathrm{E}\left[\displaystyle\sum_{t=1}^{n-h}\displaystyle\sum_{s=1}^{n-h}x_t\cdot x_{t+h}\cdot x_s\cdot x_{s+h}\right]
\end{eqnarray}
\] ホワイトノイズである \(x_t\) は互いに独立であるため、\(\mathrm{E}\left[x_t\cdot x_{t+h}\cdot x_s\cdot x_{s+h}\right]\) がゼロとならないのは \(t=s\) の場合のみ(=異なる時刻の積は期待値ゼロ)。
そこで \(t=s\) の場合を考えますと、
\[\mathrm{E}\left[x_t\cdot x_{t+h}\cdot x_t\cdot x_{t+h}\right]=E\left[x_t^2\cdot x_{t+h}^2\right]=E\left[x_t^2\right]\cdot E[x_{t+h}^2]=\sigma^2\cdot \sigma^2=\sigma^4\] 項の数は \(t=1\) から \(t=n-h\) までの \(n-h\) 個であるため、
\[\mathrm{E}\left[c_h^2\right]=\dfrac{1}{n^2}\displaystyle\sum_{t=1}^{n−h}\mathrm{E}\left[x_t^2\cdot x_{t+h}^2\right]=\dfrac{1}{n^2}\displaystyle\sum_{t=1}^{n−h}\sigma^4=\dfrac{1}{n^2}(n−h)\sigma^4\] よって、
\[\mathrm{Var}\left(c_h\right)=\dfrac{n−h}{n^2}\sigma^4\] ここで、\(n\) が \(h\) に対して十分に大きい場合、\(h\) は固定されていますので、
\[\dfrac{n-h}{n}\approx 1\]
したがって
\[\mathrm{Var}\left(c_h\right)\approx\dfrac{\sigma^4}{n}\]
続いて、自己相関 \(r_h=\dfrac{c_h}{c_0}\) の分散を求めます。
ホワイトノイズ かつ 大標本 を仮定していますので、標本分散 \(c_0\) は 前述の通り \(\sigma^2\) に収束します。
したがって、\(r_h\approx\dfrac{c_h}{\sigma^2}\) と近似できますので、
\[\mathrm{Var}\left(r_h\right)=\mathrm{Var}\left(\dfrac{c_h}{c_0}\right)\approx\mathrm{Var}\left(\dfrac{c_h}{\sigma^2}\right)=\dfrac{1}{\sigma^4}\mathrm{Var}\left(c_h\right)\] \(\mathrm{Var}\left(c_h\right)\approx\dfrac{\sigma^4}{n}\) を代入しますと
\[\mathrm{Var}(r_h)≈\dfrac{1}{\sigma^4}\cdot\dfrac{\sigma^4}{n}=\dfrac{1}{n}\] よって、標準誤差は
\[\mathrm{SE}(r_h)=\sqrt{\mathrm{Var}(r_h)}\approx\dfrac{1}{\sqrt{n}}\] と、ラグ \(h\) における標本自己相関 \(r_h\) の標準誤差は \(\dfrac{1}{\sqrt{n}}\) に近似されます。
よって
\[Z=\dfrac{\textrm{観測値}\,r_h - \textrm{帰無仮説}\mathrm{H}_0\textrm{下の期待値}\,\mathrm{E}\left[r_h\right] }{\textrm{帰無仮説}\mathrm{H}_0\textrm{下の標準誤差}\mathrm{SE}(r_h)}\approx \dfrac{r_h-0}{1/\sqrt{n}}= \dfrac{r_h}{1/\sqrt{n}}\] この標準化により \(Z\) は標準正規分布 \(\mathrm{N}(0,1)\) に従い、\(n\rightarrow\infty\) のとき \(\mathrm{E}\left[r_h\right]\rightarrow\rho_h\) となるため(漸近不偏推定量)、両側5%とする場合は、
\[\pm\dfrac{1.96}{\sqrt{n}}\]
を臨界値として帰無仮説 \(\mathrm{H_0}:\rho_h=0\) を検定することが出来ます。
サンプルサイズを 200 個、信頼区間を 95% とした場合の臨界値を確認します。
n <- 200
confidence_level <- 0.95
alpha <- 1 - confidence_level
(z_score <- qnorm(1 - alpha / 2))
z_score / sqrt(n)[1] 1.959964
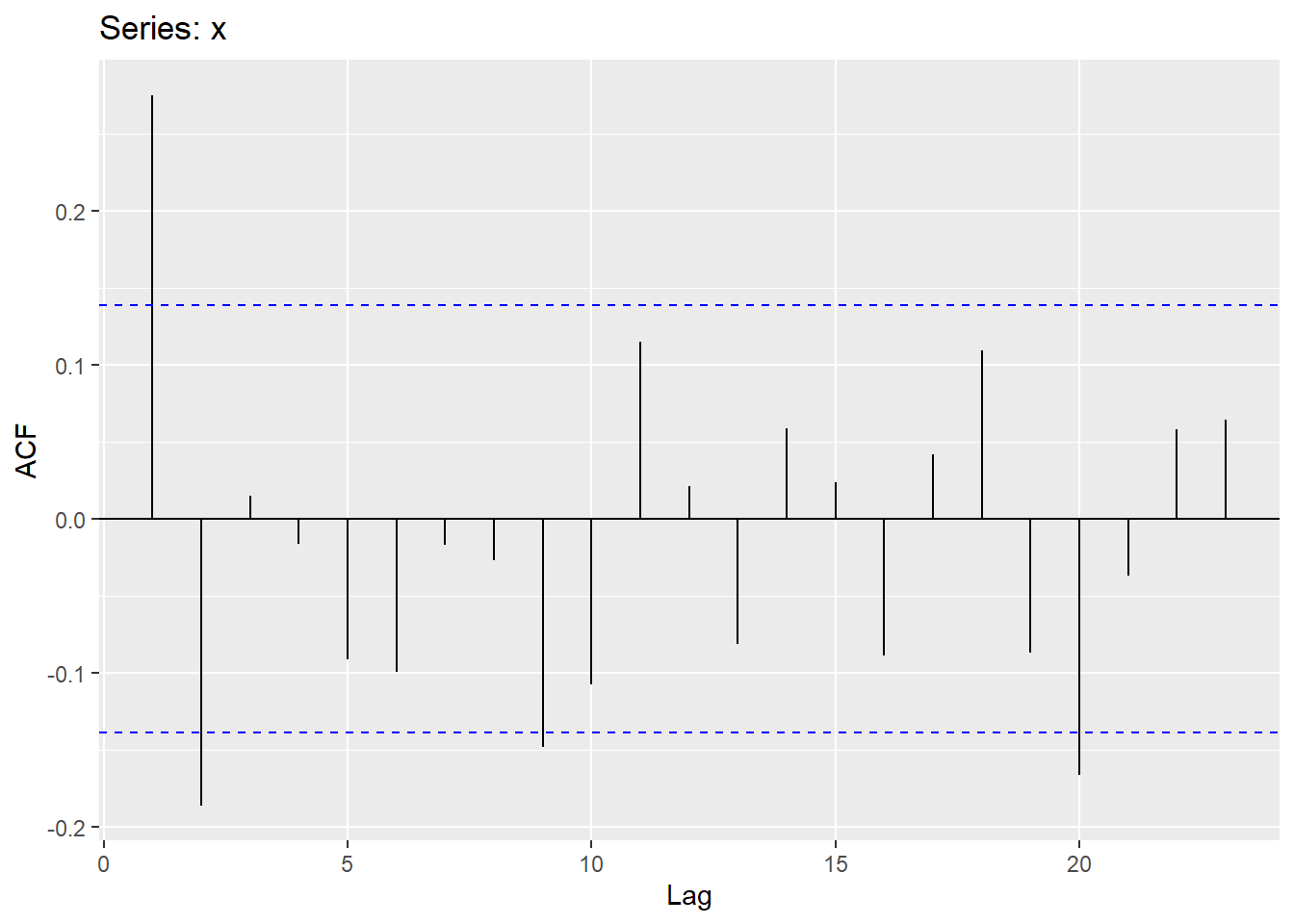
[1] 0.1385904関数 ggAcf{forecast} で引かれる臨界値ライン(Figure 1 の青色ダッシュライン)を確認します。
library(dplyr)
x <- arima.sim(model = list(ma = c(0.7, -0.5)), n = n)
forecast::ggAcf(x = x)forecast::ggAcf(x = x) %>%
{
ggplot2::ggplot_build(.)$data[[3]]
} yintercept PANEL group colour linewidth linetype alpha
1 -0.1385904 1 -1 blue 0.5 dashed NA
2 0.1385904 1 -1 blue 0.5 dashed NA一致しています。
以上です。