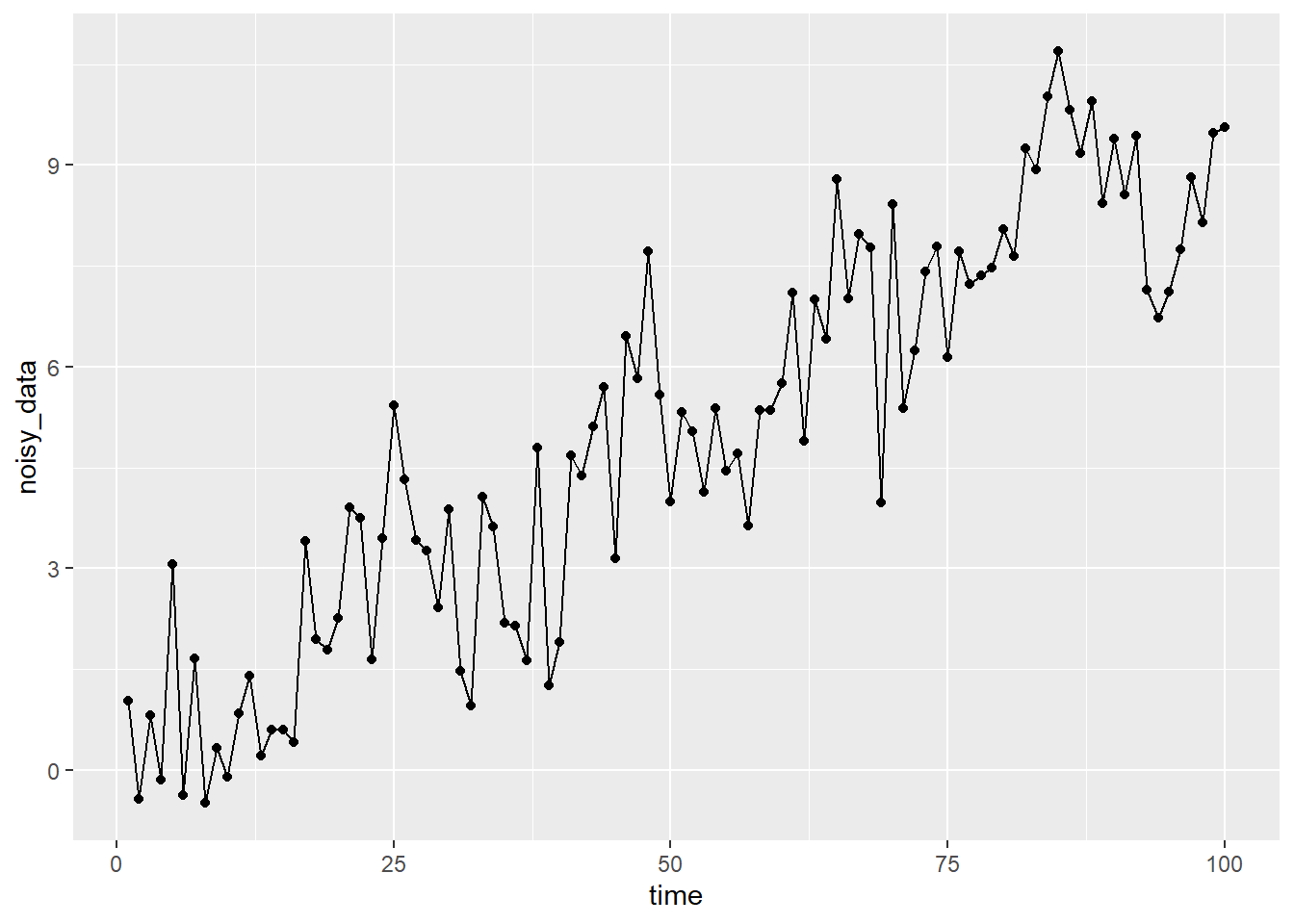Rで Savitzky-Golayフィルタ によるスムージングを試みます。
本投稿は https://chaosmemo.com/entry/2025/01/17/185654 を参照引用しています。
始めにサンプルデータを作成します。
library(ggplot2)
seed <- 20250401
set.seed(seed)
n_points <- 100
time <- seq(n_points)
original_signal <- sin(2 * pi * 0.05 * time) + 0.1 * time
noise <- rnorm(n_points, 0, 1)
noisy_data <- original_signal + noise
ggplot(mapping = aes(x = time, y = noisy_data)) +
geom_point() +
geom_line()指定した次数(degree)の多項式を最小二乗法を用いてフィッティングし、その多項式の係数を求める関数を作成します。
fit_polynomial <- function(x, y, degree) {
# x: データ点の x 座標のベクトル
# y: データ点の y 座標のベクトル
# degree: フィッティングする多項式の次数
n <- length(x)
if (n != length(y)) stop("xとyの長さが一致していません。")
if (degree >= n) stop("多項式の次数はデータ点の数より小さくなければなりません。")
X <- matrix(1, nrow = n, ncol = degree + 1)
# 計画行列 X を初期化します。
# X は n 行 (データ点の数) と degree + 1 列 (0次から degree次までの項) を持ちます。
# 最初の列はすべて 1 で、これは多項式の定数項に対応します。
if (degree > 0) { # degree が 0 より大きい場合のみループを実行
for (i in 1:degree) X[, i + 1] <- x^i
# 計画行列 X の残りの列を埋めます。
# i 列目 (i > 1) は、x の (i-1) 乗の値を格納します。
# 例えば、degree が 2 の場合、2列目は x の 1乗、3列目は x の 2乗の値になります。
# これにより、各行はデータ点における多項式の各項の値を表します。
}
XT <- t(X)
XTX <- XT %*% X
XTy <- XT %*% as.matrix(y)
if (degree == 0) {
XTX_inv <- matrix(1 / XTX[1, 1], nrow = 1, ncol = 1)
} else {
XTX_inv <- solve(XTX)
}
coefficients <- XTX_inv %*% XTy
# 多項式の係数を求めます。
# 最初の要素(coefficients[1, 1])が定数項であり、これはSavitzky-Golayフィルタにおけるスムージングされた値に対応します。
return(coefficients)
}続いて、Savitzky-Golayフィルタによるスムージングの関数を作成します。
smoothed_data_by_savitzky_golay <- function(data, window_size, poly_order) {
if (window_size %% 2 == 0 || window_size < 1) stop("ウィンドウサイズは正の奇数でなければなりません。")
if (poly_order >= window_size) stop("多項式の次数はデータ点の数より小さくなければなりません。")
m <- (window_size - 1) / 2
n <- length(data)
smoothed_data <- numeric(n)
for (i in 1:n) {
# 現在のデータ点を中心としたウィンドウのインデックスを計算
start_index <- max(1, i - m)
end_index <- min(n, i + m)
current_window_size <- end_index - start_index + 1
if (current_window_size < window_size) {
# 端のデータ点はフィルタを適用しない
smoothed_data[i] <- data[i]
next
}
# ウィンドウ内のデータとローカルなx座標を取得
window_data <- data[start_index:end_index]
local_x <- (1:current_window_size) - (i - start_index + 1) # ウィンドウの中心を0とする
# 多項式フィッティングを実行
# ウィンドウサイズが小さい場合は、多項式の次数を調整
poly_order_fit <- min(poly_order, current_window_size - 1)
coefficients <- fit_polynomial(local_x, window_data, poly_order_fit)
# スムージングされた値は、フィットした多項式の中心(ローカルx=0)での値、つまり係数の最初の要素
smoothed_data[i] <- coefficients[1, 1]
}
return(smoothed_data)
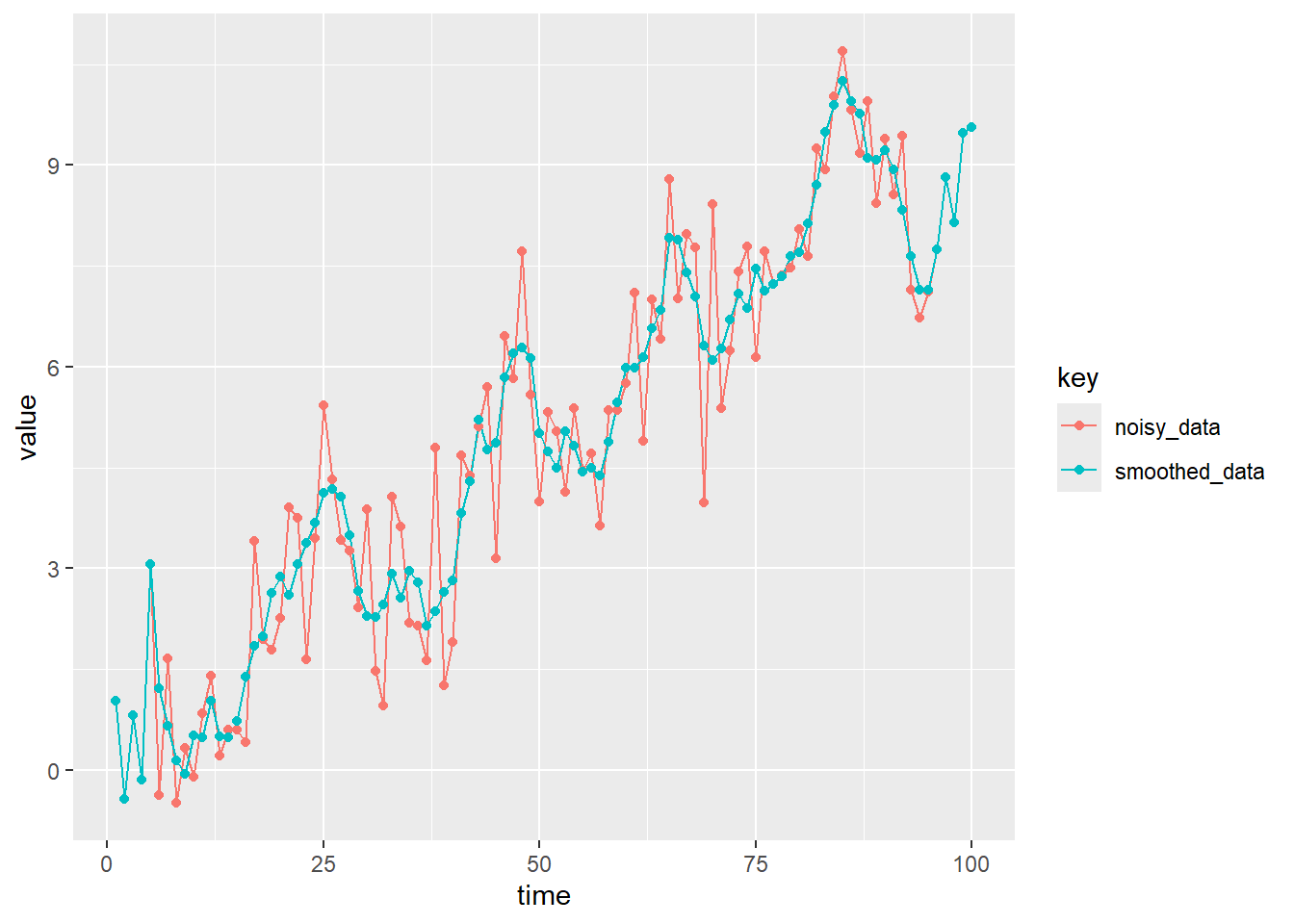
}Savitzky-Golayフィルタを適用します。
# フィルタの適用
library(dplyr)
window_size <- 11
poly_order <- 4
smoothed_data <- smoothed_data_by_savitzky_golay(noisy_data, window_size, poly_order)
data.frame(time, noisy_data, smoothed_data) %>%
tidyr::gather(, , colnames(.)[-1]) %>%
ggplot(mapping = aes(x = time, y = value, colour = key)) +
geom_line() +
geom_point()関数 sgolayfilt {signal} を利用してSavitzky-Golayフィルターを掛けます
library(signal)
smoothed_data_by_sgolayfilt <- sgolayfilt(x = noisy_data, p = poly_order, n = window_size)両者を比較します
data.frame(noisy_data, smoothed_data_by_sgolayfilt, smoothed_data, diff = round(smoothed_data_by_sgolayfilt - smoothed_data, 10)) noisy_data smoothed_data_by_sgolayfilt smoothed_data diff
1 1.0302601 0.81919823 1.03026006 -0.21106183
2 -0.4272956 0.12192701 -0.42729563 0.54922264
3 0.8075240 0.29919787 0.80752404 -0.50832617
4 -0.1413315 0.77767601 -0.14133154 0.91900755
5 3.0689512 1.15812964 3.06895121 -1.91082157
6 -0.3763657 1.21542997 1.21542997 0.00000000
7 1.6567068 0.65740614 0.65740614 0.00000000
8 -0.4942460 0.14308572 0.14308572 0.00000000
9 0.3300747 -0.05649916 -0.05649916 0.00000000
10 -0.1039824 0.50759949 0.50759949 0.00000000
11 0.8455127 0.48463921 0.48463921 0.00000000
12 1.4041576 1.03419320 1.03419320 0.00000000
13 0.2169126 0.49780893 0.49780893 0.00000000
14 0.6056208 0.48167997 0.48167997 0.00000000
15 0.5986685 0.72872009 0.72872009 0.00000000
16 0.4189924 1.38594229 1.38594229 0.00000000
17 3.4091832 1.85012529 1.85012529 0.00000000
18 1.9461318 1.99425093 1.99425093 0.00000000
19 1.7933626 2.63408036 2.63408036 0.00000000
20 2.2564416 2.87063804 2.87063804 0.00000000
21 3.9009138 2.60683013 2.60683013 0.00000000
22 3.7500969 3.05908391 3.05908391 0.00000000
23 1.6391081 3.38361454 3.38361454 0.00000000
24 3.4524806 3.68261228 3.68261228 0.00000000
25 5.4260466 4.12279745 4.12279745 0.00000000
26 4.3220107 4.18609836 4.18609836 0.00000000
27 3.4244660 4.06211569 4.06211569 0.00000000
28 3.2670941 3.48650056 3.48650056 0.00000000
29 2.4179611 2.66851681 2.66851681 0.00000000
30 3.8837429 2.28545770 2.28545770 0.00000000
31 1.4683172 2.27269998 2.27269998 0.00000000
32 0.9616992 2.45490789 2.45490789 0.00000000
33 4.0642002 2.92062686 2.92062686 0.00000000
34 3.6173006 2.56077961 2.56077961 0.00000000
35 2.1939989 2.96192253 2.96192253 0.00000000
36 2.1397165 2.79547633 2.79547633 0.00000000
37 1.6363056 2.14725240 2.14725240 0.00000000
38 4.8010143 2.36008693 2.36008693 0.00000000
39 1.2538131 2.65016149 2.65016149 0.00000000
40 1.9036753 2.82302864 2.82302864 0.00000000
41 4.6798189 3.81999548 3.81999548 0.00000000
42 4.3779563 4.28843954 4.28843954 0.00000000
43 5.1046469 5.20362310 5.20362310 0.00000000
44 5.6998983 4.75990266 4.75990266 0.00000000
45 3.1544360 4.87113253 4.87113253 0.00000000
46 6.4632310 5.83474219 5.83474219 0.00000000
47 5.8256958 6.20480313 6.20480313 0.00000000
48 7.7122591 6.28892658 6.28892658 0.00000000
49 5.5863982 6.12763173 6.12763173 0.00000000
50 3.9917342 5.01049650 5.01049650 0.00000000
51 5.3237168 4.74427603 4.74427603 0.00000000
52 5.0370372 4.49547196 4.49547196 0.00000000
53 4.1337360 5.03757097 5.03757097 0.00000000
54 5.3792986 4.82932044 4.82932044 0.00000000
55 4.4578738 4.44011525 4.44011525 0.00000000
56 4.7044637 4.50022059 4.50022059 0.00000000
57 3.6354206 4.37486266 4.37486266 0.00000000
58 5.3478402 4.87969424 4.87969424 0.00000000
59 5.3540328 5.46141878 5.46141878 0.00000000
60 5.7571611 5.97819478 5.97819478 0.00000000
61 7.1012429 5.99031253 5.99031253 0.00000000
62 4.9017807 6.14272324 6.14272324 0.00000000
63 7.0026822 6.57733484 6.57733484 0.00000000
64 6.4156720 6.84455033 6.84455033 0.00000000
65 8.7948105 7.91962126 7.91962126 0.00000000
66 7.0114217 7.88454486 7.88454486 0.00000000
67 7.9805706 7.40557162 7.40557162 0.00000000
68 7.7731898 7.04254957 7.04254957 0.00000000
69 3.9828369 6.31113638 6.31113638 0.00000000
70 8.4176453 6.10055387 6.10055387 0.00000000
71 5.3814445 6.26363893 6.26363893 0.00000000
72 6.2412910 6.70632548 6.70632548 0.00000000
73 7.4229063 7.09231380 7.09231380 0.00000000
74 7.7862779 6.87096998 6.87096998 0.00000000
75 6.1364658 7.45474500 7.45474500 0.00000000
76 7.7107395 7.12772807 7.12772807 0.00000000
77 7.2261725 7.22861953 7.22861953 0.00000000
78 7.3619992 7.34620130 7.34620130 0.00000000
79 7.4683890 7.64754212 7.64754212 0.00000000
80 8.0412209 7.69851254 7.69851254 0.00000000
81 7.6392424 8.12787726 8.12787726 0.00000000
82 9.2468682 8.70887034 8.70887034 0.00000000
83 8.9403231 9.49752168 9.49752168 0.00000000
84 10.0212898 9.88697774 9.88697774 0.00000000
85 10.6927433 10.24654279 10.24654279 0.00000000
86 9.8191700 9.94383539 9.94383539 0.00000000
87 9.1776424 9.75821033 9.75821033 0.00000000
88 9.9462135 9.11170993 9.11170993 0.00000000
89 8.4283971 9.08112438 9.08112438 0.00000000
90 9.3891153 9.22327791 9.22327791 0.00000000
91 8.5593155 8.93719406 8.93719406 0.00000000
92 9.4388376 8.33187620 8.33187620 0.00000000
93 7.1496489 7.64988481 7.64988481 0.00000000
94 6.7327313 7.14695202 7.14695202 0.00000000
95 7.1196256 7.15013585 7.15013585 0.00000000
96 7.7476933 7.47276194 7.74769330 -0.27493135
97 8.8190584 8.10905455 8.81905838 -0.71000383
98 8.1415432 8.87022628 8.14154319 0.72868309
99 9.4838473 9.46041050 9.48384732 -0.02343683
100 9.5705821 9.47666130 9.57058214 -0.09392084本投稿では 端のデータ点はフィルタを適用しない とした 端点(floor(window_size/2)) を除いて一致しています。
最後に参考として 関数 signal::sgolay によるフィルタ係数を確認します。
sgolay(p = 0, n = 5)
sgolay(p = 1, n = 5) %>% round(10)
sgolay(p = 2, n = 5) %>% round(10)
sgolay(p = 3, n = 5) %>% round(10)
sgolay(p = 4, n = 5) %>% round(10) [,1] [,2] [,3] [,4] [,5]
[1,] 0.2 0.2 0.2 0.2 0.2
[2,] 0.2 0.2 0.2 0.2 0.2
[3,] 0.2 0.2 0.2 0.2 0.2
[4,] 0.2 0.2 0.2 0.2 0.2
[5,] 0.2 0.2 0.2 0.2 0.2
attr(,"class")
[1] "sgolayFilter"
[,1] [,2] [,3] [,4] [,5]
[1,] 0.6 0.4 0.2 0.0 -0.2
[2,] 0.4 0.3 0.2 0.1 0.0
[3,] 0.2 0.2 0.2 0.2 0.2
[4,] 0.0 0.1 0.2 0.3 0.4
[5,] -0.2 0.0 0.2 0.4 0.6
attr(,"class")
[1] "sgolayFilter"
[,1] [,2] [,3] [,4] [,5]
[1,] 0.88571429 0.2571429 -0.08571429 -0.1428571 0.08571429
[2,] 0.25714286 0.3714286 0.34285714 0.1714286 -0.14285714
[3,] -0.08571429 0.3428571 0.48571429 0.3428571 -0.08571429
[4,] -0.14285714 0.1714286 0.34285714 0.3714286 0.25714286
[5,] 0.08571429 -0.1428571 -0.08571429 0.2571429 0.88571429
attr(,"class")
[1] "sgolayFilter"
[,1] [,2] [,3] [,4] [,5]
[1,] 0.98571429 0.05714286 -0.08571429 0.05714286 -0.01428571
[2,] 0.05714286 0.77142857 0.34285714 -0.22857143 0.05714286
[3,] -0.08571429 0.34285714 0.48571429 0.34285714 -0.08571429
[4,] 0.05714286 -0.22857143 0.34285714 0.77142857 0.05714286
[5,] -0.01428571 0.05714286 -0.08571429 0.05714286 0.98571429
attr(,"class")
[1] "sgolayFilter"
[,1] [,2] [,3] [,4] [,5]
[1,] 1 0 0 0 0
[2,] 0 1 0 0 0
[3,] 0 0 1 0 0
[4,] 0 0 0 1 0
[5,] 0 0 0 0 1
attr(,"class")
[1] "sgolayFilter"以上です。