Rで 誤差構造 を ベータ分布、リンク関数 を logit とする 一般化線形モデル を試みます。
本ポストは https://www.jstage.jst.go.jp/article/weed/55/4/55_4_275/_pdf を参照しています。
始めにサンプルデータを作成します。
サンプルデータは 0-100 の範囲を取る説明変数と、ベータ分布 に従い、但しスケールは説明変数と同じく 0-100 とする従属変数の組み合わせとします。
また、本ポストでは説明変数 \(X\) に対する従属変数の期待値(平均値) \(\mu\) の算出を目的とし、精度パラメータ(形状パラメータ \(\alpha\) と \(\beta\) の和 = \(\phi\) )は算出していません。
\[\begin{eqnarray}
\textrm{E}[Y]&=&\mu=\alpha/(\alpha+\beta)\\
\textrm{Var(Y)}&=&(\alpha\beta)/[(\alpha+\beta)^2(\alpha+\beta+1)]\\
\phi&=&\alpha+\beta
\end{eqnarray}\]
library(ggplot2)
seed <- 20250405
set.seed(seed)
n_obs <- 200 # サンプルサイズ
# 説明変数 X (0から100の範囲とします)
x <- runif(n_obs, 0, 100)
# 真のパラメータを設定
beta_true <- c(-2.0, 0.05) # 真の切片 (beta0) と傾き (beta1)
phi_true <- 15 # 真の精度パラメータ (phi)
# デザイン行列を作成 (切片項を含む)
X <- cbind(1, x)
# 線形予測子 eta = X * beta
eta_true <- X %*% beta_true
# 平均 mu を計算 (逆ロジット関数)
# mu = exp(eta) / (1 + exp(eta)) = 1 / (1 + exp(-eta))
mu_true <- 1 / (1 + exp(-eta_true))
# 従属変数 y を生成 (0から1の範囲のベータ分布に従う)
# ベータ分布のパラメータ shape1 = mu * phi, shape2 = (1 - mu) * phi
shape1 <- mu_true * phi_true
shape2 <- (1 - mu_true) * phi_true
y_01 <- rbeta(n_obs, shape1 = shape1, shape2 = shape2)
# データが0や1にならないように調整
epsilon <- 1e-6
y_01 <- pmax(epsilon, pmin(1 - epsilon, y_01))
# 従属変数は 0-100 のスケールとする
y_100 <- y_01 * 100
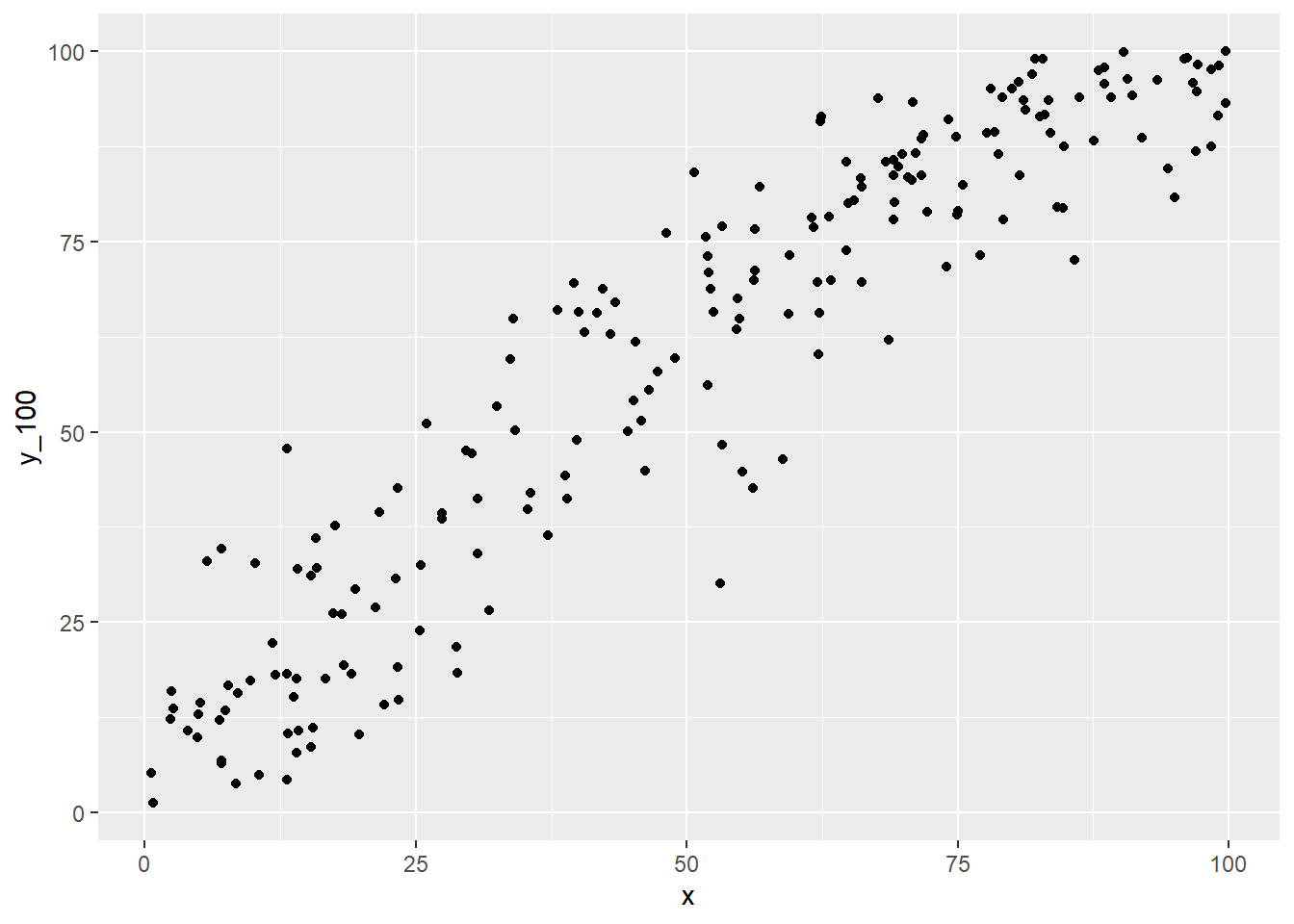
# 可視化します
(g1 <- ggplot(mapping = aes(x = x, y = y_100)) +
geom_point())続いて、Iteratively Reweighted Least Squares (IRLS) アルゴリズム を用いてパラメータ(回帰係数 \(\beta\))を推定します。
# モデルフィッティングは y_01 (0-1スケール) を使用
y <- y_01
# 初期値設定
beta_current <- rep(0, ncol(X)) # βをゼロベクトルで初期化
max_iter <- 50 # 最大反復回数
tolerance <- 1e-7 # 収束判定の閾値
for (iter in 1:max_iter) {
# (1) 線形予測子 η (eta) の計算
eta <- X %*% beta_current
# (2) 平均 μ (mu) の計算 (逆ロジット関数)
mu <- 1 / (1 + exp(-eta))
# mu が0や1にならないように調整
mu <- pmax(epsilon, pmin(1 - epsilon, mu))
# (3) リンク関数の導関数 g'(μ) の計算
# ロジットリンク g(μ) = log(μ / (1 - μ))
# その導関数 g'(μ) = 1 / (μ * (1 - μ))
g_prime_mu <- 1 / (mu * (1 - mu))
# (4) 分散関数 V(μ) の計算 (ベータ分布の場合、φを含まない部分)
# Var(y) = μ(1-μ) / (1 + φ) なので、V(μ) = μ(1-μ) とする
v_mu <- mu * (1 - mu)
# (5) IRLSの重み w の計算
# w = 1 / ( V(μ) * (g'(μ))^2 )
# w = 1 / ( (mu * (1 - mu)) * (1 / (mu * (1 - mu)))^2 )
# w = mu * (1 - mu)
# μ が 0 または 1 に近い場合(g'(μ) が大きくなる場合)には重みを小さく
# μ が 0.5 に近い場合(g'(μ) が小さくなる場合)には重みを大きく
# 注意: この重みはφを含まない形。
weights_irls <- mu * (1 - mu)
# (6) 従属変数(一時的) z の計算
# z = η + (y - μ) * g'(μ)
z <- eta + (y - mu) * g_prime_mu
# (7) 重み付き最小二乗法 (WLS) による β の更新
# β_new = (X^T W X)^(-1) X^T W z
# ここで W は weights_irls を対角成分に持つ対角行列
W <- diag(as.vector(weights_irls)) # ベクトルにしてから対角行列化
# X^T W を計算
X_T_W <- t(X) %*% W
# (X^T W X) を計算
X_T_W_X <- X_T_W %*% X
# (X^T W X)^(-1) を計算
X_T_W_X_inv <- solve(X_T_W_X)
# (X^T W z) を計算
X_T_W_z <- X_T_W %*% z
# β_new を計算
beta_new <- X_T_W_X_inv %*% X_T_W_z
# (8) 収束判定
delta <- sum((beta_new - beta_current)^2)
print(paste("Iteration:", iter, " Change in Beta:", round(delta, 8)))
beta_current <- beta_new
if (delta < tolerance) {
print(paste("収束しました (反復回数:", iter, ")"))
break
}
if (iter == max_iter) {
warning("最大反復回数に達しました。収束していない可能性があります。")
}
}
beta_estimated <- beta_current[1] "Iteration: 1 Change in Beta: 2.51005137"
[1] "Iteration: 2 Change in Beta: 0.15653074"
[1] "Iteration: 3 Change in Beta: 0.00383094"
[1] "Iteration: 4 Change in Beta: 2.32e-06"
[1] "Iteration: 5 Change in Beta: 0"
[1] "収束しました (反復回数: 5 )"推定された回帰係数 \(\beta\) です。
上段が線形予測子の切片、下段が傾きです。
beta_estimated [,1]
-2.04273337
x 0.05109242推定された従属変数( \(\hat{y}\) )を確認します。
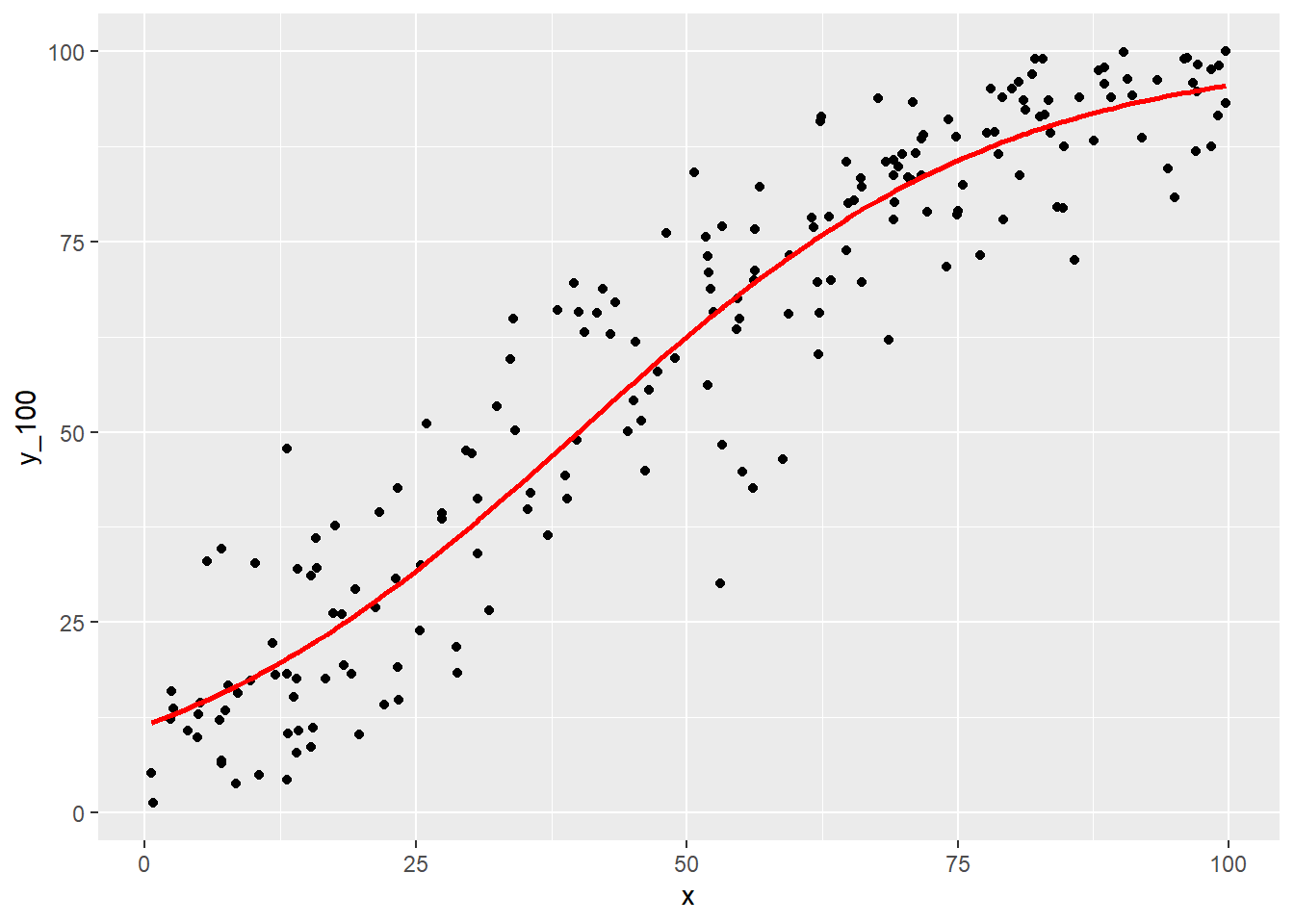
eta_pred <- X %*% beta_estimated
mu_pred <- 1 / (1 + exp(-eta_pred))
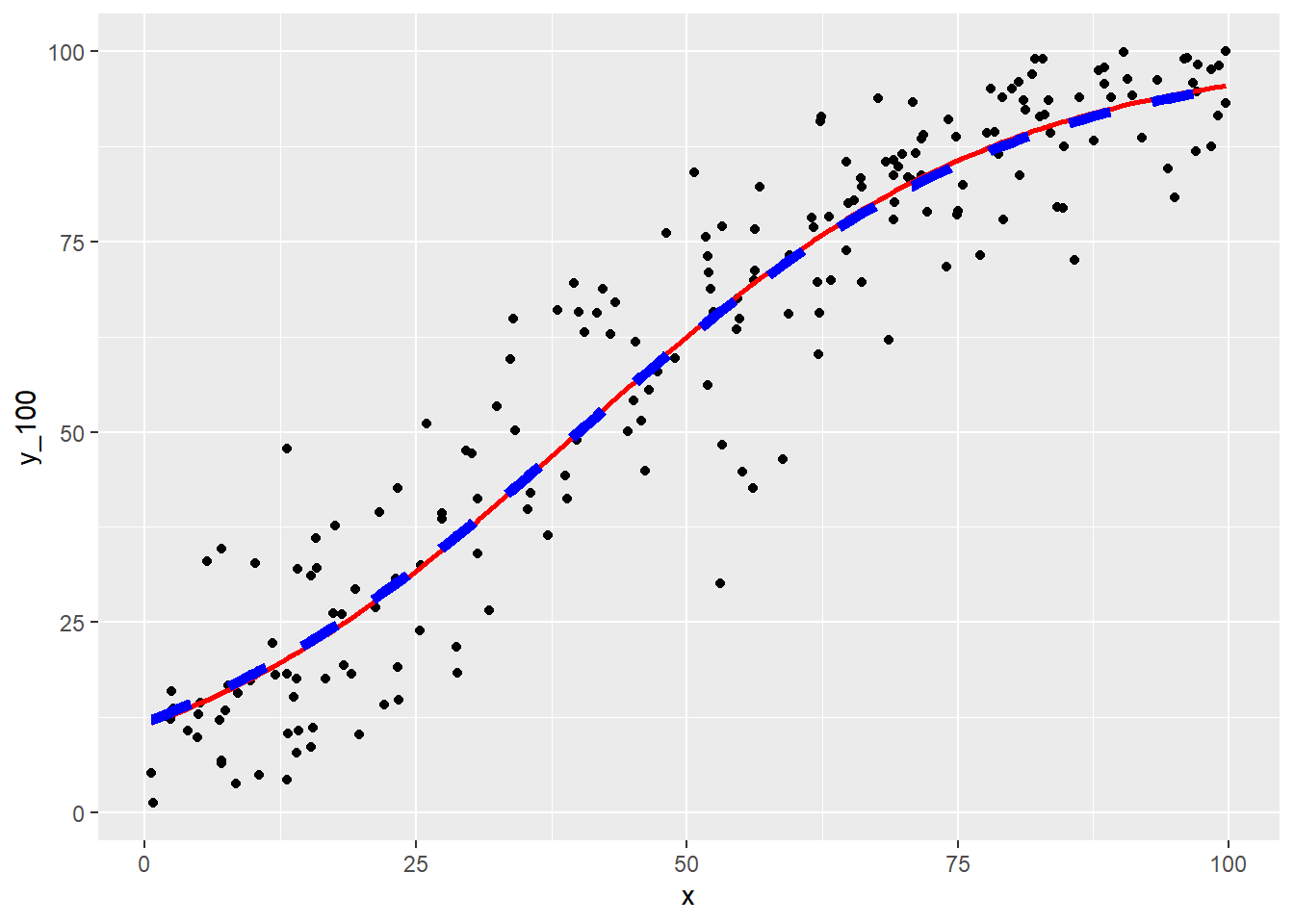
(g2 <- g1 + geom_line(mapping = aes(x = x, y = mu_pred * 100), colour = "red", linewidth = 1))真の関係と重ねます。
(g3 <- g2 + geom_line(mapping = aes(x = x, y = mu_true * 100), colour = "blue", linewidth = 2, linetype = "dashed"))Rの関数 glm の結果と比較します。
ここで、誤差構造は 疑似二項分布(quasibinomial) とします。
library(dplyr)
fit_glm_quasi <- glm(y_01 ~ x, family = quasibinomial(link = "logit"))
fit_glm_quasi %>% summary()
Call:
glm(formula = y_01 ~ x, family = quasibinomial(link = "logit"))
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -2.042733 0.089845 -22.74 <2e-16 ***
x 0.051092 0.001753 29.14 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for quasibinomial family taken to be 0.05922646)
Null deviance: 84.64 on 199 degrees of freedom
Residual deviance: 11.66 on 198 degrees of freedom
AIC: NA
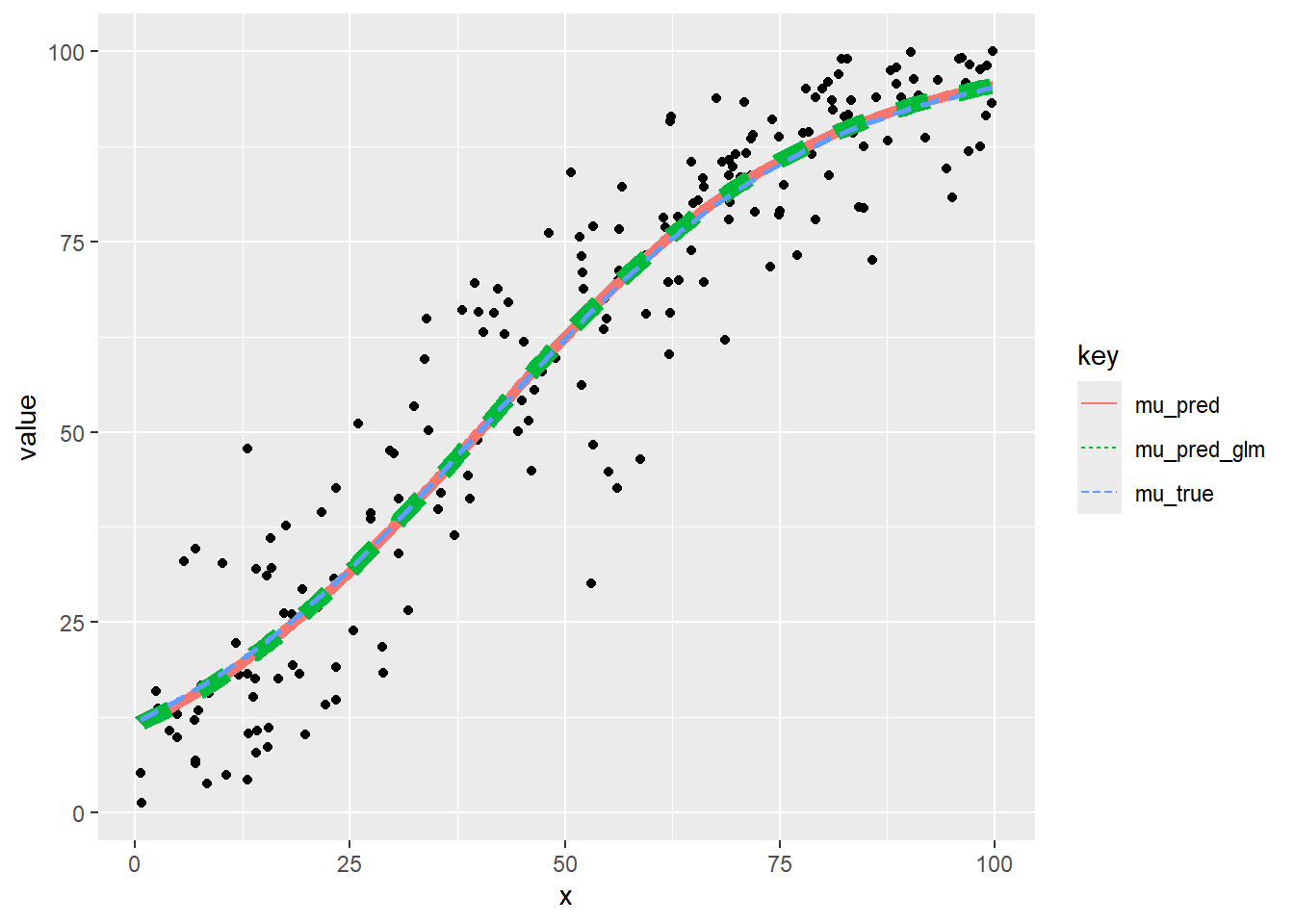
Number of Fisher Scoring iterations: 5beta_estimated と一致しています。
glm の結果と比較します。
mu_pred_glm <- predict(fit_glm_quasi, newdata = data.frame(x = x), type = "response")
unique(round(mu_pred - mu_pred_glm, 12)) [,1]
[1,] 0一致しています。
最後に全てを重ねます。
tidydf <- data.frame(x, y = y_100, mu_true = mu_true * 100, mu_pred = mu_pred * 100, mu_pred_glm = mu_pred_glm * 100) %>% tidyr::gather(, , colnames(.)[-1])
ggplot(data = tidydf, mapping = aes(x = x, y = value, colour = key)) +
geom_point(data = subset(tidydf, key == "y"), colour = "black") +
geom_line(
data = subset(tidydf, key %in% c("mu_true", "mu_pred", "mu_pred_glm")),
mapping = aes(
group = key,
linetype = key,
linewidth = ifelse(key == "mu_true", 1, ifelse(key == "mu_pred", 2, 3))
)
) +
scale_linewidth_identity(
breaks = c(1, 2, 3),
labels = c("mu_true", "mu_pred", "mu_pred_glm")
)以上です。